Рух матерiальної точки по вiдношенню до iнерцiальної системи вiдлiку, тобто такої системи, для якої справедливi основнi закони динамiки Ньютона, називається абсолютним.
Розглянемо рух матеріальної точки маси m по відношенню до неінерціальної системи відліку Оxyz, тобто до системи, яка рухається з прискоренням відносно інерціальної системи відліку О 1 x 1 y 1 z 1 (рис. 8.1).
Рух точки М вiдносно неiнерцiальної системи вiдлiку називається вiдносним.
Основна задача динамiки вiдносного руху матерiальної точки формулюється так. Нехай система вiдлiку Oxyz рухається вiдносно нерухомої системи O 1 x 1 y 1 z 1 за вiдомим законом, тобто для будь-якого моменту часу нам вiдомi прискорення апер = а o точки O, а також переносна кутова швидкiсть ωпер i переносне кутове прискорення εпер системи вiдлiку Oxyz вiдносно системи вiдлiку O 1 x 1 y 1 z 1. Знаючи сили, якi дiють на точку М, а також початковi умови руху точки М i системи вiдлiку Oxyz, потрiбно знайти закон вiдносного руху точки М.
|

Для розв’язання цiєї задачi треба спочатку скласти диференцiальне рiвняння вiдносного руху точки М, а потiм, проiнтегрувавши це рiвняння, знайти закон вiдносного руху точки.
За другим законом Ньютона для руху точки вiдносно iнерцiальної системи вiдлiку
m 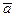 =
= 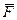 +
+  , (8.1)
, (8.1)
де 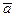 - абсолютне прискорення точки М,
- абсолютне прискорення точки М, 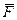 - рiвнодiйна активних сил, дiючих на точку М,
- рiвнодiйна активних сил, дiючих на точку М, 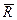 - реакцiя в’язi.
- реакцiя в’язi.
Абсолютне прискорення точки за теоремою Корiолiса:
 , (8.2)
, (8.2)
де aвід, aпер, aкор - вiдносне, переносне i корiолiсове (поворотне) прискорення точки М вiдповiдно.
Пiдставимо в рiвняння (8.1) значення прискорення  з (8.2) i одержимо
з (8.2) i одержимо
m  =
= 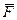 +
+  + (- m
+ (- m  ) + (- m
) + (- m  ). (8.3)
). (8.3)
Сила, рiвна добутку маси рухомої точки та її переносного прискорення i направлена протилежнo цьому прискоренню, називається переносною силою iнерцiї  :
:
 = - m
= - m  . (8.4)
. (8.4)
Сила, рiвна добутку маси рухомої матерiальної точки та її корiолiсового прискорення i направлена протилежно цьому прискоренню, називається корiолiсовою або поворотною силою iнерцiї  :
:
 = - m
= - m  . (8.5)
. (8.5)
Рiвняння (8.3) можна переписати так:
m  =
= 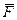 +
+  +
+  +
+  . (8.6)
. (8.6)
Це рiвняння є основним законом динамiки в векторнiй формi для вiдносного руху невiльної матерiальної точки. В загальному випадку
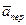 =
=  +
+  ´(
´(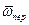 ´
´  ) +
) +  ´
´  ; (8.7)
; (8.7)
 = 2(
= 2( ´
´  ), (8.8)
), (8.8)
де  - радiус-вектор, що визначає положення матерiальної точки М вiдносно початку O рухомої системи Oxyz.
- радiус-вектор, що визначає положення матерiальної точки М вiдносно початку O рухомої системи Oxyz.
Порiвнюючи рiвняння (8.6) i (8.1), приходимо до такого висновку: основне рiвняння динамiки вiдносного руху матерiальної точки можна скласти так, як i основне рiвняння динамiки абсолютного руху точки (8.1), якщо тiльки до дiючих на точку сил 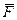 i
i  додати переносну i корiолiсову сили iнерцiї
додати переносну i корiолiсову сили iнерцiї  і
і  .
.
В проекцiях на осi системи вiдлiку Oxyz маємо
 =
=  ,
,  =
=  ,
,  =
=  ;
;

 (8.9)
(8.9)
 .
.
Аналогiчно можна одержати рiвняння вiдносного руху точки в проекцiях на осi натурального тригранника.
Розглянемо вiдносний спокiй тiла поблизу Землi. На пiдвiшений до нитки тягар дiють двi сили: сила притягання тiла Землею 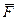 i сила натягу нитки
i сила натягу нитки  . Сила
. Сила 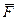 направлена по радiусу до центра земної кулi i, згiдно закону всесвiтнього тяжiння, дорівнює
направлена по радiусу до центра земної кулi i, згiдно закону всесвiтнього тяжiння, дорівнює

Завдяки добовому обертанню Землi пiдвiшений до нитки тягар перебуває в рiвномiрному русi по колу радiуса r = Rз cos φ i, отже, на тягар дiє доцентрова сила mω 2 r, яка направлена до центра С кола добового обертання.
У даному разi доцентрова сила mω 2 r є геометричною сумою сил 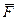 i
i  (рис. 8.2).
(рис. 8.2).

Рис. 8. 2.
Лiнiя, вздовж якої розмiщується висок (нитка з тягарем), називається вертикаллю.
Вертикаль утворює з площиною екватора кут θ, який називається географiчною широтою того мiсця, де пiдвiшений тягар (див. рис. 8.2).
Основне рiвняння вiдносного спокою одержимо з рiвняння (8.6), якщо в ньому прийняти
vвід = 0; aвід = 0;  = - m· 2(
= - m· 2(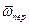 ´
´ 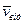 )= 0,
)= 0,
що дає
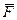 +
+  +
+  = 0. (8.10)
= 0. (8.10)
З рівняння (8.10) бачимо, що вiдносний рух iснує тодi, коли прикладенi сили 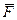 i
i  зрiвноваженi переносною силою iнерцiї
зрiвноваженi переносною силою iнерцiї  .
.
Отже, у випадку вiдносного спокою матерiальної точки геометрична сума трьох сил - активної 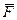 , пасивної
, пасивної  i переносної сили iнерцiї
i переносної сили iнерцiї  - дорiвнює нулю.
- дорiвнює нулю.
Вага тiла
Формула сили ваги:  = m
= m 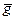 . Вагу тiла можна вимiрювати на пружинних терезах. Це вимiрювання визначає, однак, не силу притягання тiла до Землi, а лише ту частину
. Вагу тiла можна вимiрювати на пружинних терезах. Це вимiрювання визначає, однак, не силу притягання тiла до Землi, а лише ту частину  цiєї сили
цiєї сили 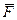 , яка проявляється статично, бо зважування на терезах не дає змоги виявити другу частину сили
, яка проявляється статично, бо зважування на терезах не дає змоги виявити другу частину сили 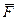 , яка проявляється в переносному прискореннi ω 2 r тiла, зумовленому добовим обертанням тiла разом із Землею.
, яка проявляється в переносному прискореннi ω 2 r тiла, зумовленому добовим обертанням тiла разом із Землею.
Вага тiла, згiдно з її означенням, дорiвнює (рис. 8.3):
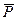 =
= 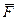 - m
- m  . (8.11)
. (8.11)
На полюсi доцентрова сила дорiвнює нулю i сила ваги дорiвнює силi притягання 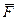 , тобто
, тобто  =
= 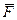 . Вага тiла на екваторi найменша i дорiвнює Р = F- mω 2 Rз. За другим законом Ньютона
. Вага тiла на екваторi найменша i дорiвнює Р = F- mω 2 Rз. За другим законом Ньютона 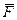 = m
= m  , де
, де  - абсолютне прискорення тiла.
- абсолютне прискорення тiла.
Значить
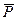 = m
= m  - m
- m 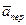 = m (
= m ( -
-  ) = m
) = m  , (8.12)
, (8.12)
де позначено
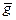 =
=  -
-  . (8.13)
. (8.13)
Абсолютне прискорення 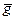 0 можна визначити з рiвностi
0 можна визначити з рiвностi
γ (mM/R3 2)·( 3/R3) = m
3/R3) = m  , (8.14)
, (8.14)
де  3/R3 - одиничний вектор, напрямлений вiд тiла М до центра Землi;
3/R3 - одиничний вектор, напрямлений вiд тiла М до центра Землi;
 = γ (M/R3 2)·(
= γ (M/R3 2)·( 3/R3). (8.15)
3/R3). (8.15)

Рис. 8. 3.
Значить
g 2 = (g 0 -  )2 = g 02 - 2 g 0
)2 = g 02 - 2 g 0  +
+  .
.
Оскiльки  = ω 2 R3 cos φ, то
= ω 2 R3 cos φ, то

Нехтуючи пiд радикалом останнiм доданком, що має множником ω 4, i добуваючи наближено квадратний корiнь, матимемо:
g = g 0 -ω 2 R3 cos2 φ. (8.16)
Для полюса φ = π /2, g 0 = 983см/с2; ω 2 R3≈ 3см/с2, а тому формулу (8.16) можна записати так:
g = (983 -3cos2 φ) см/с2.
Однак справжнi вимiрювання показують, що
g = ( 983 -5,2cоs2 φ) см/с2.
На практицi користуються середнiм значенням g = 981 см/с2. У зв’язку з впровадженням мiжнародної системи одиниць СI введено так зване нормальне значення g, яке позначають g н; за означенням приймають g н= 9,80665 м/с2.
 2020-08-05
2020-08-05 133
133








