Малі коливання механічної системи з декількома ступенями вільності

 

Тут досліджуються малі коливання механічних систем, на які накладені голономні ідеальні та стаціонарні в’язі. Розглянемо систему з двома ступенями вільності. Узагальнені координати - q ₁ і q ₂. Кінетична енергія системи дорівнює

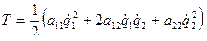       (19.11)

Величини а ₁₁, а ₁₂, а ₂₂ називають інерційними коефіцієнтами. Рівняння Лагранжа другого роду мають вигляд

            (19.12)

З урахуванням (19.11) рівняння (19.12) перепишемо так:

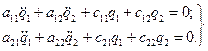      (19.13)

Частинний розв’язок рівнянь (19.13) шукаємо у вигляді:

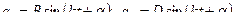(19.14)

де В, D, α - невідомі сталі. Для їх визначення знаходимо похідні від (19.14), скориставшись рівняннями (19.13), і одержимо

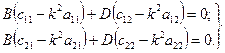       (19.15)

Система рівнянь має відмінні від нуля розв’язки, якщо детермінант системи буде рівний нулю:

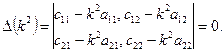       (19.16)

 

З рівнянь (19.15) знаходимо відношення амплітуд

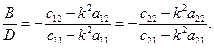      (19.17)

З виразів (19.16) або (19.17) знайдемо рівняння частот (по іншому його називають віковим рівнянням):

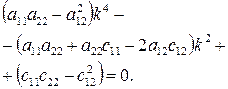   (19.18)

Досліджувані рухи будуть малими, рівновага буде стійкою, якщо корені цього рівняння будуть додатними:

Якщо  чи  від’ємні або є комплексними величинами, то розв’язки (19.14) включають гіперболічні функції і рух навколо положення рівноваги не буде малим. Корені  і  будуть додатними тоді, коли виконуються нерівності

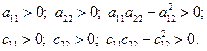
Після того, як корені рівняння частот k ₁ і k ₂ обчислені, знаходимо головні коливання системи. Перше головне коливання описується рівняннями

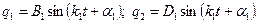(19.19)

Друге головне коливання описується рівняннями

  (19.20)

Загальний розв’язок

  (19.21)

Відношення амплітуд дорівнює

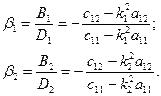              (19.22)

Тоді

(19.23)

Довільні сталі інтегрування D ₁, D ₂, α ₁, α ₂ визначаються з початкових умов. При розв’язанні задач на дослідження малих коливань консервативної системи з двома ступенями вільності рекомендується такий порядок дій:

1) вибрати узагальнені координати q ₁ і q ₂;

2) обчислити кінетичну енергію системи Т;

3) обчислити потенціальну енергію системи П або узагальнені сили;

4) знайти похідні від кінетичної енергії і скласти рівняння Лагранжа другого роду;

5) задати частинний розв’язок і підставити його в систему диференціальних рівнянь руху;

6) з одержаної в пункті 5) системи алгебраїчних рівнянь визначити амплітуди коливань і знайти рівняння частот;

7) розв’язати рівняння частот, знайти власні частоти коливань системи;

8) внести знайдені частоти в частинний розв’язок і одержати формули, які описують два головних коливання;

9) додавши рівняння головних коливань для кожної узагальненої координати, знайти загальний розв’язок;

10) з початкових умов знайти чотири довільні сталі інтегрування.

 

Зауваження. Для закріплення матеріалу §19 (пунктів 19.1 – 19.3) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 53.2, 53.4, 53.5, 54.1 - 54.5, 55.1 - 55.5, 55.7;

2) № 48.10, 48.19, 48.20, 48.35 - 48.37, 48.39, 53.6, 53.12 - 53.14, 54.10, 54.12, 54.20, 54.22, 54.32, 54.35, 55.9, 55.12, 55.15 – 55.17, 55.25;

3) № 53.15 - 53.18, 54.37 - 54.39, 54.40, 54.42, 54.48, 55.28, 55.36, 55.41, 55.44.

Рекомендується розв’язати також задачі № 14.5, 14.7, 14.15, 14.17, 14.28, 14.31, 14.38, 14.61, 14.63, 14.65, 14.75, 14.78, 14.82, 14.89 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Стійкість руху

 

Стійкість руху - поняття, яке характеризує тривале (довгочасне) зберігання будь-яких характеристик руху системи. Проблема стійкості руху виникає при вивченні гіроскопічних систем, систем автоматичного регулювання (наприклад, слідкуючих систем), коливних рухів, при дослідженні рухів літаків, ракет і т. д.. Ж.- Л. Лагранж вважав, що механічна система знаходиться в рівновазі, якщо під час руху відстані між її точками залишаються скінченними. Відомі визначення стійкості руху, які давали С.- Д. Пуассон, П.- С. Лаплас, М. Є. Жуковський та ін. Найбільш загальним і важливим за своїм застосуванням є визначення, яке дав стійкості руху О. М. Ляпунов. Рух будь-якої механічної системи можна обчислити теоретично, знаючи діючі на неї сили і початкові умови. Рух, який система згідно цих обчислень повинна здійснювати по Ляпунову, називається незбуреним рухом. Але практично система зазнає випадкових впливів, які не були враховані при обчисленнях. Якими б малими і короткочасними не були б ці впливи, вони приведуть до того, що в деякий момент t=t ₀ координати і швидкості точок системи одержать малі, але нерівні нулю прирости, які Ляпунов називає початковими збуреннями. Подальший рух називається збуреним рухом. Якщо при малих збуреннях деякі з характеристик руху в збуреному русі мало відрізняються від тих значень, які були в незбуреному русі, то по Ляпунову незбурений рух є стійким по відношенню до цих характеристик руху. Якщо при малих діях (збуреннях) значення розглядуваної характеристики буде в збуреному русі з часом все більше відхилятись від її значення в незбуреному русі, то незбурений рух є по відношенню до даної характеристики нестійким. Умови, при яких розглядуваний рух є стійким, називаються умовами (критеріями) стійкості.

В якості прикладу розглянемо рух симетричного вертикального гіроскопа (рис. 19.1).

Теоретично його вісь повинна залишатись вертикальною при будь-якій кутовій швидкості 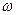. Однак фактично, коли 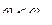( 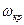- критична кутова швидкість), будь-яке збурення (поштовх) приводить до все зростаючого відхилення від вертикалі; якщо ω>ω_кp, то малі збурення практично не позначаються на напрямі осі. Отже, при ω<ω_кp гіроскоп по відношенню до напряму його осі буде нестійким, а при ω>ω_кp – стійким. Це і є умовою стійкості. При цьому

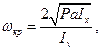      (19.24)                

Рис. 19. 1.

 

 

 

де Р - вага гіроскопа, a – відстань від точки О до центра ваги С, І_x і І_y - моменти інерції гіроскопа відносно осей Ох і Оу відповідно. Іншим буде результат, якщо розглянути рух гіроскопа по відношенню до кута обертання φ навколо осі Oz. В незбуреному русі при відсутності тертя (опору) кут повороту φ=ωt. Якщо внаслідок поштовху кутова швидкість зміниться на величину ε, то в збуреному русі φ ₁ = (ω+ε) t. Різниця Δ φ=φ ₁ - φ= =εt  не залежить від ω і з часом нескінченно зростає; тоді по відношенню до кута повороту φ рух гіроскопа буде нестійким при будь-яких значеннях кутової швидкості ω. Таким чином, один і той же рух по відношенню до одних з його характеристик може бути стійким, а по відношенню до інших - нестійким.

 

  Дослідження положень відносної рівноваги.

Часто при дослідженні різних механізмів потрібно знайти положення відносної рівноваги і стійкість. Для цього складають так звану змінену потенціальну енергію системи W:

W=П+T,                                 (19.25)

де П - потенціальна енергія, Т - кінетична енергія системи. Стан рівноваги (положення рівноваги) визначається з рівняння

                             (19.26)

 

Положення рівноваги буде стійким при

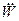>0.                               (19.27)

При 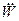                             <0                                (19.28)

положення рівноваги є нестійким.

 

Дослідження стійкості руху по першому наближенню.

Метод визначення стійкості руху по першому наближенню полягає в наступному. Нехай

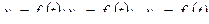        (19.29)

є частинними розв’язками системи диференціальних рівнянь першого порядку

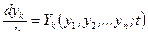                 (19.30)

при заданих початкових умовах руху

  при t ₀=0.     (19.31)

Розв’язок (19.29) визначає незбурений рух системи. При інших початкових умовах руху значення змінних у_k, які визначають подальший рух системи, записують так:

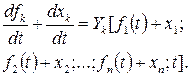        (19.32)

Віднімемо від (19.32) рівняння (19.30) і знайдемо

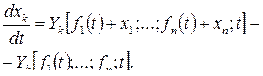(19.33)

Введемо позначення:

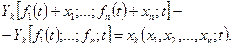(19.34)

Одержимо систему диференціальних рівнянь

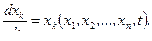                (19.35)

З (19.34) виходить, що

x_k (0, 0,...,0; t) = 0                          (19.36)

(х ₁ = х ₂ =...= х_n = 0)                          (19.37)

є частинним розв’язком системи (19.35), який відповідає незбуреному рухові.

Для розгляду стійкості руху по першому наближенню в системі рівнянь (19.35) в правій частині виділяють лінійні складові (доданки). Коли час явно не входить в праву частину рівняння, будемо мати

        (19.38)

Запишемо характеристичне рівняння системи (19.38):

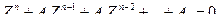     (19.39)

Згідно першої теореми Ляпунова, незбурений рух, який визначається рівнянням (19.29), є стійким, коли корені характеристичного рівняння (19.39) мають від’ємну дійсну частину. В цьому випадку нелінійні доданки в правій частині рівнянь (19.38) не впливають на стійкість руху. Про знак кореня характеристичного рівняння можна судити на основі теореми Гурвіца, яка формулюється так: рівняння n -го степеня з дійсними коефіцієнтами (а ₀>0)

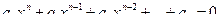    (19.40)

має всі корені з від’ємною дійсною частиною, коли всі визначники вигляду

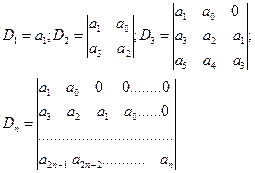
є додатними.

При розв’язуванні задач на дослідження стійкості руху системи по першому наближенню рекомендується такий порядок дій:

1) визначаємо число ступенів вільності системи і вибираємо узагальнені координати;

2) користуючись рівнянням Лагранжа, складаємо рівняння незбуреного руху;

3) складаємо рівняння збуреного руху, вважаючи, що узагальнені координати відрізняються від значень в незбуреному русі на величини першого порядку малості;

4) віднімаємо від диференціальних рівнянь збуреного руху відповідні рівняння незбуреного руху;

5) для системи лінійних диференціальних рівнянь з постійними коефіцієнтами складаємо характеристичне рівняння;

6) користуючись теоремою Гурвіца, визначаємо знаки дійсних частин коренів характеристичного рівняння і потім робимо висновок про стійкість руху системи.

 

Зауваження. Для закріплення матеріалу §19 (пункт 19.4) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 56.1 - 56.5;

2) № 56.7 – 56.15;

3) № 56.17 - 56.20.

Рекомендується розв’язати також задачі № 18.6, 18.7, 18.10, 18.12, 18.15, 18.19, 18.20, 18.24, 18.26, 18.27, 18.32 зі збірника  “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Теорія удару