Проведение касательных к окружности

Введение

 

Занятия геометрическими построениями предполагают умение грамотно пользоваться чертёжными инструментами и материалами. И хотя в настоящее время  для получения чертежей в основном используют графические прикладные пакеты (AutoCAD, ArchiCAD, Компас и др.), научиться традиционным приёмам начертания и познакомиться с основными геометрическими построениями будущему проектировщику необходимо, поскольку графические операции, выполняемые с помощью чертёжных инструментов, развивают изобретательность, инициативу и конструктивные способности, а кроме того, способствуют повышению  его геометрической культуры.

  Совершенствуя глаз и руку, приучая их к получению строго определённых сочетаний линий при решении различных конструктивных задач, можно развить аккуратность в начертании, столь необходимую в процессе проектирования, а также укрепить дисциплину собственного мышления, выраженную в его логической форме.

Материал в данной работе поделен на два раздела. В первом разделе приведены общие сведения об окружности,  рассматриваются её основные свойства и  построения, связанные с нею (проведение касательных, спрямление дуг, деление окружностей на равные части, построение сопряжений, обводов и др.).

Во втором разделе, меньшем по объёму, обсуждаются некоторые виды геометрических орнаментов и общие принципы их построения, основанные по большей части на идее симметрии.

Многие геометрические построения, включённые в данную работу, встречаются как при решении курсовых графических работ(КГР), выполняемых в течение всех трёх семестров изучения Инженерной графики, так и при решении задач, предлагаемых на СРСП в порядке подготовки к экзамену по любой из дисциплин –  ИГ - 1, ИГ - 2 или ИГ - 3.

Кроме того, часть рассмотренных задач,  не получивших достаточного отражения в современной учебной литературе по инженерной графике, но представляющих интерес для практиков, мы сочли полезным включить в данную работу.

   При описании решений всех приводимых задач, доказательная часть их из методических соображений практически опущена.

В Приложении дано краткое описание КГР №3, выполняемой в  системе дисциплины ИГ-2, приводятся варианты заданий на построение сопряжений.

 

Раздел 1

Окружность.

 

   1.1. Основные факты

 

· Точка есть окружность с бесконечно-малым радиусом.

· Прямая есть окружность с бесконечно-большим радиусом.

· Окружность можно задать тройкой линейно независимых точек.

· Окружность можно задать тройкой различных прямых.

· Через точку вне окружности можно провести к ней не более двух касательных, каждая из которых перпендикулярна радиусу, проведённому в точку касания; такой радиус называют нормалью.

· Из всех точек на окружности ближайшая к внешней точке S и наиболее удалённая от S, есть основания нормалей к окружности, проходящих через S.

· Окружность имеет бесчисленное множество осей симметрии, проходящих через её центр.

· Диаметр, перпендикулярный хорде, делит эту хорду и каждую из стягиваемых ею дуг пополам.

· Геометрическое место середин взаимно параллельных хорд есть диаметр, перпендикулярный этим хордам.

· Две окружности не могут иметь более двух общих точек.

· Линия, соединяющая центры двух пересекающихся окружностей, перпендикулярна общей хорде этих окружностей и делит её пополам.

· Если две окружности имеют одну общую точку, то они касаются друг друга и точка касания лежит на линии центров.

· Вписанный в окружность угол равен половине дуги, на которую он опирается.

· Угол, образованный касательной и хордой с концом в точке касания, равен половине дуги, отсекаемой этой хордой.

· Геометрическое место точек, расположенных по одну сторону от прямой, из которых данный отрезок этой прямой виден под одним и тем же углом, есть дуга окружности, концы которой совпадают с концами данного отрезка.

 

 1.2. Простейшие задачи  для самостоятельного  решения

 

     При решении задач на построение, чаще всего применяется метод

геометрических мест,  известный из  школьного курса геометрии.

Ниже приводится несколько испытательных задач для самостоятельного решения с применением чертёжных инструментов.

 

Задача 1. Через т. М внутри окружности построить наименьшую хорду.

Задача 2. Через т. М внутри окружности построить хорду, равную данному

        отрезку АВ.

Задача 3.  Построить хорду заданной окружности, равную и параллельную

              данному отрезку LK.

Задача 4. Построить вписанный прямой угол, стороны которого проходят

        через заданные внутри окружности точки А и В. Сколько решений

        может иметь задача? Может ли задача вообще не  иметь решений?

Задача 5.  Построить отрезок, равный и параллельный заданному отрезку

        CD, концы которого лежали бы на данной прямой m и данной

         окружности k.

Задача 6.   Построить отрезок, равный и параллельный данному отрезку MN,

              концы которого лежали бы на двух данных окружностях.

 

Проведение касательных к окружности

     Задачи на проведение касательных к окружности часто встречаются при построении контуров различных декоративных и архитектурных элементов (орнаментальных композиций, ваз, скоций, гуськов, карнизов, кронштейнов и т.д.). При этом задача на проведение касательной сводится к построению на окружности точки (точек) касания.

    

Задача 1. Через т. М провести касательную к окружности k (рис. 1).

1. Соединяем тт. С и М прямой и делим отрезок СМ пополам точкой Р.

2. Строим окружность b радиуса РС из т. Р.

3. Находим тт. А и В пересечения окружностей k и b; это – точки касания.

4. Через тт. А и В проводим касательные t_a и t_b. Проведение нормалей n ясно

    из чертежа. 

 

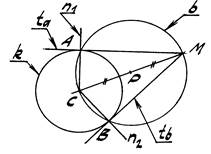
                                                     Рис. 1

 

Построение касательной, как видно из решения задачи, возможно лишь при

наличии центра Р, который даже за неимением  центра С   заданной дуги k, удаётся отыскать.

 

Задача 2. Через т. Е провести касательную к дуге окружности k (рис. 2).

1. Через т. Е проведём две произвольные прямые так, чтобы заданная дуга

пересеклась с каждой из них в двух точках – А,В и С,D.

2. Делим каждый из полученных отрезков пополам точками 1 (А1=В1) и 2

 (С2=D2).

3. Находим середины Т и L отрезков 1Е и 2Е соответственно.

1. Центр Р лежит на пересечении перпендикуляров, проведённых через тт. Т и   L.
2. Проводим из т. О окружность l радиуса R=О1=О2. Дальнейшее ясно из чертежа.

                                

                  

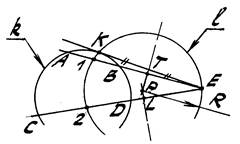
                                                              Рис. 2

 

Задача 3. Через т. F провести касательные tⁱ к окружности k (рис. 3).

Для решения задачи используется свойство полярного соответствия,

которое  известно так же как принцип  взаимности (см. в любом курсе Проективной геометрии).

1. Через т. F проведём три произвольные секущие 1-2,   3-4 и 5-6.

3. Построим прямую, проходящую через диагональные точки М и N.

4. Полученная прямая пересечёт окружность k в точках касания А и В.

5. Из т. F через тт. А и В проведём касательные t_a и  t_b.

Построение принципиально не изменится, если т. F окажется несобственной

(рис. 4).

 

 

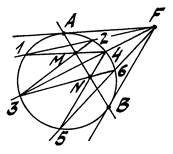
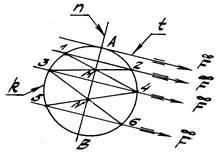
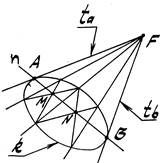
   Рис. 3                              Рис. 4                                 Рис. 5

 

 

Данный способ может успешно применяться при построении касательных и к другим кривым 2-го порядка, например, к эллипсу (рис. 5).                   

 

Задача 4.  Через т. К  на дуге с окружности провести к этой дуге   касательную t (рис. 6).

1. Дугой произвольного радиуса из т. К наметим на дуге с тт. 1 и 2.

2. Параллельно хорде 1-2 проведём через т. К искомую касательную t.                                                

                                

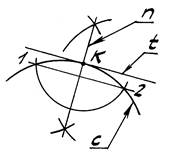
                                                   Рис. 6

 

 1.4. Спрямление окружности

Задача 1. Спрямить дугу АВ окружности с известным центром О (рис. 7).

1. Соединим концы дуги и, тем самым, получим хорду АВ.

2. Через центр О дуги проведём прямую, перпендикулярную хорде.

3. На этой прямой от  т. О  отложим  вправо отрезок ОЕ=2R  и

     полученную т. Е, соединим с концами дуги А и В.

4. Через т. С проведём к дуге касательную, параллельную АВ; на ней

продолжения прямых ЕА и ЕВ отсекут отрезок А^' В^', который с

достаточным   приближением и будет  равен длине дуги АВ.

Этот способ даёт минимальные погрешности при угле дуги φ<40^○. Его в 15 в.  предложил  кардинал Николай Кузанский (Nicolaus Cusanus).

                          

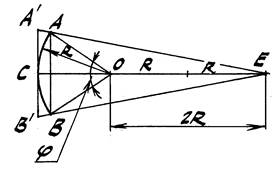
                                                        Рис. 7

 

Задача 2. Спрямить полуокружность АВ (рис. 8).

1. Проведём в т. В касательную t к окружности и из центра О к диаметру АВ

 проведём прямую m под углом φ=30^○.

2. В пересечении прямых t и m  находим т. Е.

3. От т. Е на касательной откладываем отрезок ЕD=3R, который

приближенно равен длине полуокружности АВ.

На рис. 9 аналогичная задача решена несколько иначе. Предлагается разобрать её самостоятельно, анализируя несложный чертёж.

 

                                              

 

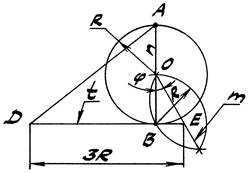
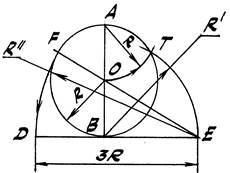
                            Рис. 8                                                 Рис. 9

 

Задача 3. Определить длину дуги МN, если центр её неизвестен (рис. 10).

1. Делим хорду МN на четыре равные части.

2. Одну четверть откладываем от т. N на дуге МN.

3. Найденную т. Е соединяем с точкой деления 1.

4. Удваивая отрезок Е1 до отрезка ЕК, получаем спрямлённую длину

дуги МN.

                                         

 

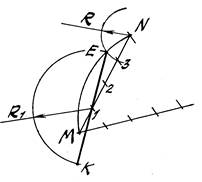
                                                    Рис. 10