Практически для построения прямоугольной аксонометрии окружности, расположенной в координатной плоскости (или плоскости уровня), строят овалы, условно аппроксимирующие эллипсы в прямоугольной аксонометрии. Работа с ними намного упрощает (и ускоряет!) процесс построения аксонометрических изображений, содержащих круглые формы (рис. 39).
a) 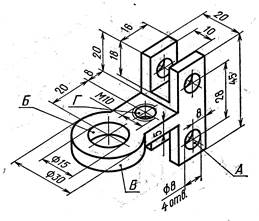 b)
b) 
Рис. 39
Задача 1. Построить прямоугольную изометрию окружности k радиуса R, расположенной в горизонтальной плоскости π'2 (рис. 40 a,b).
1. Строим окружность с центром в т. О', через которую проводим аксонометрические оси x', y ' и z' (рис. 40 a).
a)  b)
b) 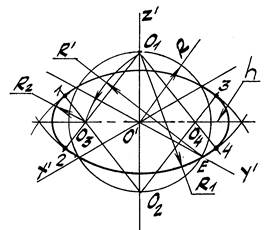
Рис. 40
2. Отмечаем точки пересечения О1 и О2 окружности и оси z' (рис. 40 b).
3. Из т. Е пересечения оси y' и данной окружности проводим дугу радиуса R'= ЕО1 до её пересечения с горизонтальной прямой h в т. О3.
4. Находим т. О4, симметричную О3.
Дальнейшее построение четырехцентрового овала с точками стыка 1, 2,
3 и 4 понятно из рис. 40 b.
Следует заметить, что ориентация овалов в разных аксонометрических плоскостях (или плоскостях, параллельных им), а также соотношения величин их осей, зависит от направления стороны треугольника следов, расположенной в соответствующей аксонометрической плоскости.
|
|
|
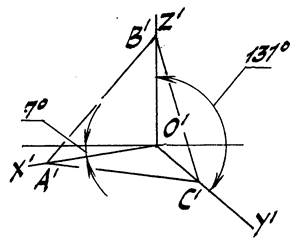
Например, если овал на рис. 40 b располагать на аксонометрических плоскостях в изометрии (рис. 41), то:
· большая ось h овала, расположенного в плоскости π'1 будет параллельна следу А'В' треугольника следов А'В'С' (рис. 41);
· большая ось h овала, расположенного в плоскости π'2 будет параллельна следу А'С';
· большая ось h овала, расположенного в плоскости π'3 будет параллельна
следу В' С'.
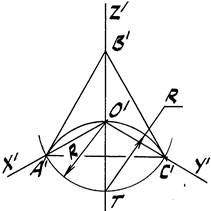
Рис. 41
При этом овалы в изометрии, лежащие в разных аксонометрических плоскостях равны при равенстве большой оси овала 1,22 d, а малой – 0,58 d, где d – диаметр исходной окружности.
В других видах аксонометрии соотношения величин осей овалов в разных аксонометрических плоскостях, могут различаться.
Задача 2. Построить прямоугольную диметрию окружности k, радиуса R, лежащей в горизонтальной плоскости π'2 (рис. 42).
1. Строим окружность заданного радиуса R с центром в т. О'.
2. От тт. А и В её пересечения с осью z' откладываем вверх и вниз отрезки
АО1= ВО2 =R.
3. Находим тт. 1 и 2 пересечения заданной окружности с осью х'.
4. Соединяем тт. 1 и 2 с центрами О1 и О2.
5. В пересечении горизонтальной прямой m É О' с прямыми О11 и О22
находим ещё два центра – О3 и О4.
Применяя их для построения дуг, как показано на рис. 37, строим овал,
большая и малая оси которого с достаточным приближением равны
|
|
|
соответственно 2.12R и 0.7R.
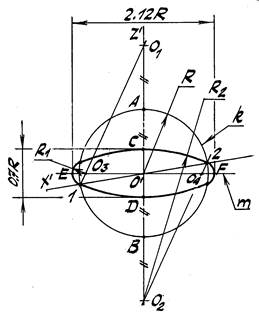

Рис. 42 Рис. 43
На рис. 43 для построения прямоугольной диметрии окружности того же радиуса R, лежащей во фронтальной плоскости π'1, через концы 1, 2, 3 и 4 (точки стыка) сопряжённых диаметров, параллельных осям х' и z' проводим горизонтальные прямые, которые пересекают взаимно-перпендикулярные оси МN и LК овала в четырёх центрах – О1, О2, О3 и О4. Окончательное проведение четырёхцентровой кривой несложно уяснить из чертежа.
Следует иметь в виду, что ось LК овала в плоскости π'2 параллельна диметрической оси y' и равна 1,9R, другая ось MN равна 2,12R. Обе величины с достаточным приближением соответствуют осям эллипса, лежащего в плоскости π'1.
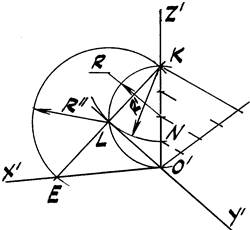
Дополнение. Построение углов между осями в прямоугольной диметрии в «приведённом» виде (рис. 44 а) выполняется следующим образом (рис. 44 b):
1. На оси z' от заданного начала О' откладываем отрезок О'К.
2. На отрезке О'К как на диаметре строим полуокружность радиуса R.
3. Из т. К проводим дугу радиуса R'= КN=3 / 4 О'К.
4. На пересечении двух дуг находим т. L, которая вместе, с т. О' определит ось у'.
5. Из т. L проведём полуокружность радиуса R'', которая пересечёт прямую КL в т. Е (КL=LЕ).
6. Искомая ось х' проходит через тт. ЕО'.
а) b)
Рис. 44
3.3. Построение циркульных спиралей
Точка, которая вращается в плоскости около некоторого центра и удаляется от него по определённому закону, описывает траекторию, представляющую собою спираль. Спирали относятся к односвязным линиям, не имеющим никаких разветвлений и простирающимся до бесконечности. Спирали широко используются в архитектурном декоре и имеют долгую художественную и сакральную традицию.
Циркульная спиральная кривая, состоящая из последовательных сопряжённых дуг, называется завитком.
Задача 1. Построить завиток по двум центрам 1 и 2 – концам заданного отрезка (рис. 45).
1. Из центра 1 проводим полуокружность 1'-2 радиуса R1, равного величине исходного отрезка 1-2.
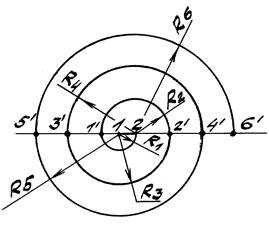

Рис. 45 Рис. 46
2. Из центра 2 проводим полуокружность 1'-2' радиуса R2.
3. Из центра 1 проводим полуокружность 2'-1' радиуса R3.
Дальнейшие построения аналогичны и их легко понять из чертежа.
Задача 2. Построить завиток по трём центрам 1, 2 и 3 – вершинам равностороннего треугольника (рис. 46).
1. Из центра 1 проводим дугу 3-1', равную трети окружности радиуса R1.
2. Из центра 2 проводим дугу 1'-2', равную трети окружности радиуса R2.
3. Из центра 3 проводим дугу 2'-3', равную трети окружности радиуса R3.
Дальнейшие построения несложно продолжить аналогичным образом.
Задача 3. Построить завиток по четырём центрам 1, 2, 3 и 4 – вершинам квадрата (рис. 47).

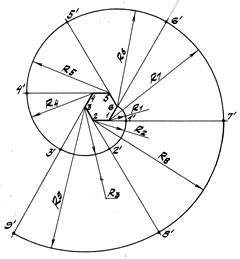
Рис. 47 Рис. 48
1. Из центра 1 проводим дугу 4-1' радиуса R1, равного стороне исходного квадрата.
2. Следующую дугу 1'-2' радиуса R2 проводим из центра 2.
3. Очередную дугу 2'-3' проводим из центра 3 радиусом R3 .
Далее построения выполняются сходным образом, при этом на каждом этапе центры сопряжения сменяются последовательно (в данном случае, по часовой стрелке).
Построение шестицентрового завитка предлагается разобрать самостоятельно (рис. 48).
Задача 4. Построить завиток по заданному диаметру 4-4' окружности с известным центром О (рис. 49).
|
|
|
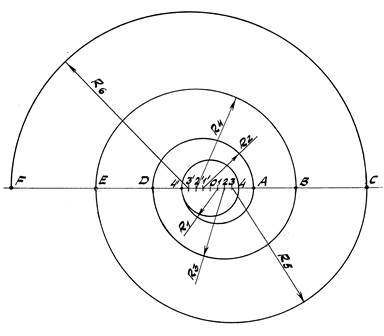
Рис. 49
1. Поделим заданный диаметр 4-4' на n равных частей по n / 2 на радиус.
2. Тогда при n=8 радиусом R1=1-4' из точки 1 проводим
полуокружность 4'–А.
3. Радиусом R2 =1'-А из точки 1' проводим полуокружность АD.
4. Далее из центра 2 проводим полуокружность DB радиусом R3 = D-2.
Последующие построения проводятся аналогичным образом.
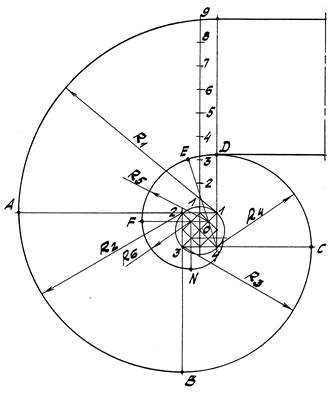
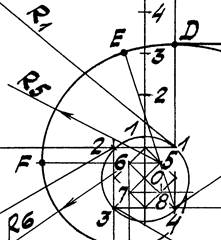
Задача 5. Построить завиток по заданному отрезку ОА, где О – центр завитка (рис. 50 a, b).
1. Делим отрезок ОА на n равных частей, например на n=9.
2. Около центра О описываем окружность радиуса, равного 1 / 9 ОА,
и вписываем в неё квадрат 1 - 2 - 3 - 4 (обход вершин против часовой
стрелки).
a) b)
Рис. 50
3. Соединяем середины сторон полученного квадрата и, таким образом,
находим ещё один квадрат, вписанный в предыдущий, в который, в свою очередь, аналогичным образом вписываем очередной квадрат 5 - 6 - 7 - 8 (обход вершин также против часовой стрелки) и т.д. (рис. 50 b).
4. Строим дугу 9-А радиуса R1= 1 - 9 из центра 1; т. А лежит на продолжении
стороны квадрата 1 - 2.
5. Строим дугу АВ радиуса R2=2 - А, причем т. В лежит на продолжении
стороны 2-3 квадрата. Далее построения ведутся аналогичным образом.
Точку Е стыка двух смежных дуг радиусов R4 и R5 находим на продолжении отрезка 4 - 5.
Спираль можно строить также на основе золотого прямоугольника (рис. 51), в котором отношение большей стороны к меньшей равно золотой пропорции, т.е.
АВ / ВС = 1+ 
В этом прямоугольнике его стороны АВ и DC делятся точками О и Т1 в отношении 5 / 3. В результате прямоугольник оказывается разделённым на квадрат АОТ1 D и прямоугольник ОВСТ1 стороны ОТ1 и ВС которого, в свою очередь, так же делятся в отношении 5 / 3. Очередной и последующие прямоугольники продолжают делить аналогичным образом.
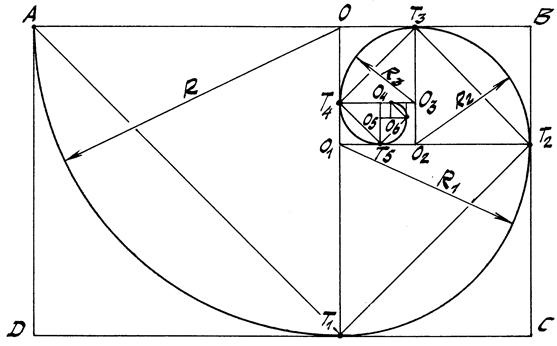
Рис. 51
В каждом квадрате, полученном таким образом, можно последовательно провести дуги окружностей из центров О, О1, О2, О3, О4, О5, …, которые образуют завиток, построение которого традиция приписывает Архимеду.
|
|
|
3.4. Дополнение: сопряжения, выполняемые посредством коник
Кривые 2-го порядка (коники) широко применяются в технике строительстве и архитектуре. Форма коники и её положение на плоскости определяются заданием пяти параметров, например, пятью касательными, никакие три из которых, не должны пересекаться в одной точке или пятью точками, никакие три из которых не должны лежать на одной прямой. В число пяти параметров может входить любая комбинация из касательных и точек, отвечающих указанным выше условиям.
При задании коники пятью параметрами вид кривой (эллипс, парабола или гипербола) предусмотреть заранее трудно. Поэтому кривую удобнее задавать двумя касательными к ней с точками касания на них и графическим или инженерным дискриминантом.
Пусть касательные ta и tb касаются кривой в тт. А и В и пересекаются в т. М (рис. 52).
Найдём середину Т хорды АВ и проведём медиану МТ. Выберем на медиане некоторую точку N и зададим тем самым значение дискриминанта. Тогда коника может считаться заданной.
Дискриминантом f коники называется отношение отрезков NM к ТМ, т.е. f= NM/ ТМ. При этом, если f < 0,5, то кривая будет эллипсом, если f = 0,5 – параболой, а если f > 0,5 – гиперболой.
Задача 1. Построить некоторое множество текущих точек кривой k, которая определена парой касательных с точками А и В на них и дискриминантом f= NM/ ТМ (рис. 53).
Поскольку при подсчёте величина дискриминанта окажется, в нашем случае, равной f = 0,42, то искомой кривой будет эллипс. Для построения эллипса необходимо отыскать некоторое множество его текущих точек в следующем порядке:
1. Проводим прямые a =А  N и b = В
N и b = В  N.
N.
2. Через т. М проводим произвольную прямую l, которая пересечёт прямые
a и b соответственно в точках 1 и 2.
3. Точку Е кривой находим на пересечении прямых с (А-2) и d (В-1).
4. Пучок прямых li c центром в т. М позволяет найти сколько угодно
точек Еi кривой при аналогичных построениях.

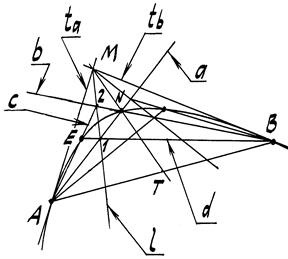
Рис. 52 Рис. 53
Задача 2. Построить арочную кривую, которая определена парой взаимно-параллельных касательных ta и tb с точками касания А и В на них и точкой N подъёма (рис. 54).
Поскольку дискриминант f= N 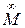 / Т
/ Т 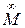 , при несобственной точке
, при несобственной точке 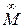 будет f < 0,5, то арочный свод – эллиптическая кривая. Таким образом АВ – большая ось эллипса, TN – его малая полуось и нахождение его текущих точек окажется аналогичным предыдущей задаче.
будет f < 0,5, то арочный свод – эллиптическая кривая. Таким образом АВ – большая ось эллипса, TN – его малая полуось и нахождение его текущих точек окажется аналогичным предыдущей задаче.
1. Проводим прямые a =А  N и b = В
N и b = В 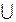 N.
N.
2. Между А и В проводим произвольно прямую l ║ ТN, которая пересечёт
прямые a и b соответственно в точках 1 и 2.

Рис. 54
3. Точку Е кривой находим на пересечении прямых А-2 и В-1.
4. Переместив прямую l в положение l', аналогичными построениями
найдём ещё одну текущую т. Е' и т.д. Пучок параллельных прямых li,
проходящих через несобственную т. 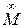 позволяет найти сколько
позволяет найти сколько
угодно точек Еi кривой.
 2020-08-05
2020-08-05 1694
1694








