2020-08-05
447
Система называется полной, если любая логическая функция может быть выражена через три основные логические функции: конъюнкцию, дизъюнкцию и отрицание. Логические функции можно разделить на три основных типа: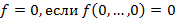 
; 
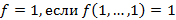и самодвойственная функция, если 
.
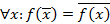В таблице истинности наборы значений переменных упорядочены по их возрастанию, иными словами, по увеличению их десятичных аналогов, тогда логическая функция называется монотонной, если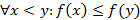 
.
Для логической функции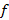 
ее полином Жегалкина имеет вид
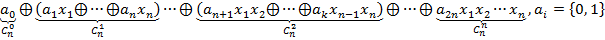
Переменные в каждом слагаемом связанны конъюнкцией. Полином Жегалкина для логических функций находится однозначно. Если для логической функции 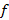в полиноме Жегалкина 
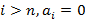, тогда в слагаемых отсутствуют произведение переменных, тогда функция является линейной. Все рассмотренные выше функции – замкнутые, тогда в результате применения логических операций получим функцию того же класса.
Система булевых функций полна, если она не лежит целиком в рассмотренных классах, иными словами, среди функций имеются не сохраняющие постоянное значение, не линейные и не монотонные. Если хотя бы одной из таких функций в одной взятой системе нет, тогда система – неполная, при этом некоторые булевые функции невозможно представить, используя только функции этой переменной.
Для составления полинома Жегалкина функции n переменных, следует сначала записать ее общий вид с учетом всех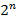 
слагаемых с заранее неизвестными коэффициентами. Подстановка значений 
обнуляет все элементы, кроме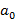 
, тогда получаем значение 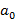по значению функции. С учетом найденного 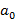подставим 
и получим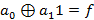 
, где подстановка 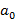позволит найти 
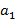. Подстановка всех наборов значений переменных позволит найти все коэффициенты полинома Жегалкина, если присутствует хотя бы одной слагаемое с произведением, иными словами, логическая функция не линейна.
Если с помощью функций систем можно описать все функции системы, тогда новая система также является полной – следствие теоремы Поста. Можно показать, что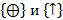 
являются двумя полными системами из одной функции. Для этого достаточно с учетом констант и этой функции записать отрицание одной переменной и конъюнкцию или дизъюнкцию двух переменных.
Если логических функций несколько и для одной из них выполняются условия теоремы Поста, тогда независимо от остальных система является полной.
