Эквивалентность состояний конечных автоматов и эквивалентность конечных автоматов

       Бинарное отношение 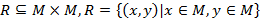, при этом  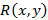часто задается в виде 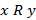. В логике высказываний бинарное отношение называют двуместным предикатом.

       Бинарные отношения обладают следующими свойствами:

1. Рефлективность, если 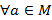, тогда выполнено ;

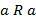2. Транзитивность, если 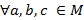, тогда выполнено ;

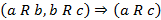3. Симметричность, если 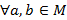, тогда выполнено ;

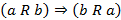4. Антисимметричность, если 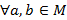, тогда выполнено ;

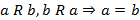Бинарное отношение R является отношением эквивалентности, если оно рефлективное, транзитивное и симметричное. Если отношение R является отношением эквивалентности, тогда каждое множество элементов можно разбить на классы эквивалентности.

       Чтобы разбить элементы множеств отношения эквивалентности необходимо зафиксировать первый элемент и перебрать остальные с включением в первый класс, из чего следует, что класс не пустой, поскольку первый элемент находится в отношении с самим с собой. Аналогично действуем со всеми элементами множества. Конечное множество в итоге разобьется на классы не более его мощности.

       Разбиение на классы эквивалентности поможет в проверке конечных автоматов на эквивалентность и их минимизации. Состояние 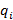 конечного автомата  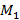эквивалентно состоянию  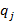тогда и только тогда, когда автомат, начав работу в состоянии  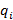будет допускать в точности те же цепочки или слова, что и в состоянии 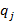. Если существует цепочка или слово языка 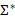, которая допустима из одного состояния и недопустима из другого, тогда цепочка является различающей два этих состояния.

       Если два состояния конечного автомата являются эквивалентными, тогда в таблице переходов этого автомата можно одно из этих состояний исключить, заменяя переходы в него названием другого состояния. Можно в матрице переходов у каждого состояния указывать дополнительно значение F в виде единицы, если состояние конечно или ноль, ели состояние не конечно.

Теорема: Каждый регулярный язык распознается конечным автоматом, в котором каждое состояние достижимо из некоторого начального состояния и из каждого начального состояния достижимо хотя бы одно конечное состояние. При этом распознавание некоторого языка в конечном автомате можно исключить недостижимое из начальных состояний конечные состояния автомата.

       Слово или цепочка 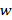 различает состояния  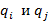автомата, если при такой входной цепочке из одного состояния завершается конечным состоянием, а для другого конечным не является. Если цепочка  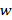различает состояния при одинаковом входном состоянии a, тогда строка  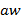различает состояния  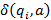и .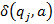

       Для логических функций имеется конечное число входных наборов, что позволяет минимизировать их по одному из критериев сложности. Для конечных автоматов протяженность входных цепочек не ограничена, что исключает метод простого перебора.

       Минимизация конечных автоматов начинается удалением состояний, недостижимых из начальных состояний и удалением состояний, из которых не достигаются конечные состояния. Для полученных состояний классы эквивалентности составляются следующим образом: в один класс вносятся конечные состояния, среди которых в новый класс выделяются те, из которых в конечное состояние можно достичь за один переход. В последующие классы вносятся конечные состояния, достижимые за два, три и т.д. переходов.