2020-08-05
1098
Основу действий с логическими функциями описал Буль. Часто логические переменные и логические функции называют булевыми. Логическая функция ставит соответствие n-мерному вектору элемент из двухэлементного множества 
. Обычно логическую функцию описывают таблицы истинности, где при n переменных содержится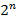 
строк. Построение таблицы истинности рассмотрено в введении в данный раздел. Логические функции представляются как логические операции в логических выражениях. Для логических операций также используют диаграммы Эйлера-Вена.
Основными логическими функциями являются
1. Дизъюнкция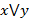 
– выражение, которое принимает значение 1, если хотя бы один из переменных равен 1. Дизъюнкция – логическое сложение, обозначаемое как 
.
2. Конъюнкция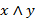 
– выражение, которое принимает значение 1, если обе переменные равны 1. Конъюнкция – логическое умножение.
3. Логическое следствие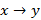 
– принимает значение 0 только верном посыле 
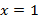и неверном заключении 
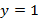. Логическое следствие – импликация.
4. Логическое равенство (эквивалентность) 
– принимает значение 1 только при одинаковых значениях переменных.
5. Логическое неравенство (строгая дизъюнкция) 
– принимает значение 1 только при различных значениях переменных.
Логические функции обладают следующими свойствами
1. 
;
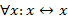2. 
;
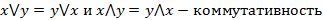3. 
;
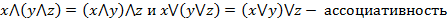4. 
;
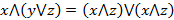5. 
;
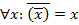6. 
;
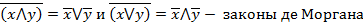7. 
.
Основываясь на данных свойствах логических функций, можно получить следующие соотношения
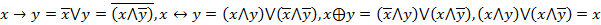
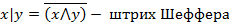
Иными словами, можно любую логическую функцию записать с применением конъюнкции, дизъюнкции и отрицания, которые называют основными булевыми функциями.
Пользуясь перечисленными свойствами и тождествами, можно упрощать запись логических функций, предварительно сведя неосновные логические функции к основным. Таким образом, можно выполнять дальнейшие действия с логическими функциями от любого числа переменных.
Используя описанный принцип, можно составлять совестно-заданную переключательную функцию при анализе сложных высказываний и проверке логичности вывода.
