2020-08-05
99
В предыдущих главах конечный автомат описывался как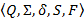 
, где F – множество конечных состояний. Вместо него можно ввести новую функцию – функцию выхода вида 
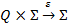, описывающую выходной алфавит. Данная функция в паре значений 
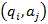ставит в соответствие букву выходного алфавита, который может совпадать с входным алфавитом. При этом при описании автомата необходимо кроме перехода в новое состояние с учетом входного символа, следует указать символ на выходе.
Кодирование состояний входных и выходных сигналов исходного состояния происходит следующим образом:
1. Для входных символов кодирование состояния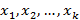 
в виде набора 
;
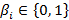2. Для текущего состояния значения переменных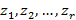 
в виде набора 
;
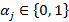3. Код следующего состояния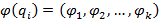 
со значениями 
;
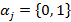4. Выходной символ 
кодируется как 
.
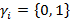При этом кодирование можно провести различными способами. Возможно, что некоторые последовательности символов могут оказаться неиспользованными. В таком случае значение функций следующего состояния и выходного символа будут заданы не на всех двоичных наборах значений переменных.
Обычно, стараясь получить более удобные результаты, используют минимальную дизъюнктивную и конъюнктивную нормальную форму логической функции. Для описания конечного автомата составляется таблица, в которой по кодам входных символов и текущего состояния указываются кода соответствующих значени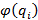й 
и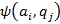 
. В этой таблице имеется 
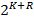строк и 
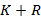столбцов.
В первых столбцах указываются наборы кодов, соответствующих паре состояние – входной символ. Каждому набору кодов в первых столбцах указываются сначала коды для нового состояния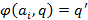 
и код для соответствующего выходного сигнала. По составленной таблице можно построить диаграмму Мура этого конечного автомата.
При заполнении всех столбцов такой таблицы, именно доопределив недостающие кода значени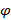й 
и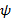 
, можно конечный автомат задавать системой логических функций 
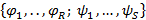в количестве 
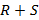штук. Каждую из них можно представить как совершенную конъюнктивную или дизъюнктивную форму, минимизируя полученный результат.
