Вариант 1
• 1. Решите уравнение: а) х 3 - 81х = 0; б) 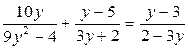 .
.
•2. Решите неравенство: а) 2 х 2 - 13 х + 6 < 0; б) х 2 > 9.
• 3. Решите неравенство методом интервалов:
а) (х + 8) (х - 4) (х - 7) > 0; б)
• 4. Решите биквадратное уравнение х 4 - 19 х 2 + 48 = 0.
5. При каких значениях т уравнение 3 х 2 + тх + 3 = 0 имеет два корня?
6. Найдите область определения функции 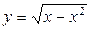 .
.
7. Найдите координаты точек пересечения графиков функций у = 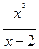 и y = x 2 - 3 x +1.
и y = x 2 - 3 x +1.

Контрольная работа №3 по алгебре в 9 классе
По теме «Уравнения и неравенства с одной переменной»
Вариант 2
• 1. Решите уравнение: а) x 3 - 25 x = 0; б) 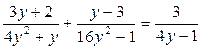 .
.
• 2. Решите неравенство: а) 2 х 2 - х - 15 > 0; б) х 2 < 16.
•3. Решите неравенство методом интервалов:
а) (х + 11) (х + 2) (х - 9) < 0; б) 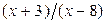 > 0.
> 0.
• 4. Решите биквадратное уравнение х 4 - 4 х 2 - 45 = 0.
5. При каких значениях п уравнение 2 х 2 + пх + 8 = 0 не имеет корней?
6. Найдите область определения функции 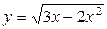
7. Найдите координаты точек пересечения графиков функций y = 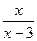 и
и
y = 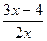 .
.
Контрольная работа №4 по алгебре в 9 классе
По теме «Уравнения и неравенства с двумя переменными»
Вариант 1
 • 1. Решите систему уравнений:
2 x + y = 7,
х 2 - у = 1. • 1. Решите систему уравнений:
2 x + y = 7,
х 2 - у = 1.
| • 2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м2. Найдите стороны прямоугольника. |
•3. Изобразите на координатной плоскости множество решений системы неравенств:
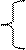 х 2 + у 2 х 2 + у 2 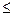 9,
y 9,
y 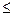 x + 1. x + 1.
| 4. Не выполняя построения, найдите координаты точек пересечения параболы у = х 2+ 4 и прямой х + у = 6. |
5. Решите систему уравнений:
 2 y - х = 7,
2 y - х = 7,
х 2 – ху - у 2 = 20.
Вариант 2
 • 1. Решите систему уравнений
x - 3 y = 2,
xy + y = 6. • 1. Решите систему уравнений
x - 3 y = 2,
xy + y = 6.
| • 2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120 см2. |
•3. Изобразите на координатной плоскости множество решений системы неравенств:
 x 2 +у 2 x 2 +у 2 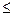 16,
х + у 16,
х + у 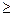 -2. -2.
| 4. Не выполняя построения, найдите координаты точек пересечения окружности х 2 + у 2 = 10 и прямой х + 2 у = 5. |
5. Решите систему уравнений:
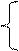 y - 3 x = l,
y - 3 x = l,
х 2 - 2 ху + у 2 = 9.
Контрольная работа №5 по алгебре в 9 классе
По теме «Арифметическая прогрессия»
Вариант 1
• 1. Найдите двадцать третий член арифметической прогрессии (а n), если а 1 = -15 и d = 3.
• 2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0;....
3. Найдите сумму шестидесяти первых членов последовательности (b n),заданной формулой b n = 3 п - 1.
4. Является ли число 54,5 членом арифметической прогрессии (а n),в которой а 1 = 25,5 и а 9= 5,5?
5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.
Вариант 2
• 1. Найдите восемнадцатый член арифметической прогрессии (а n),, если
а 1 = 70 и d = -3.
• 2. Найдите сумму двадцати первых членов арифметической прогрессии:
-21; -18; -15;....
3. Найдите сумму сорока первых членов последовательности (b n),заданной формулой b n= 4 п - 2.
4. Является ли число 30,4 членом арифметической прогрессии (а n),в которой
а 1 = 11,6 и а 15 = 17,2?
5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.
 2020-09-24
2020-09-24 163
163








