Лекция №3.
Тема: Дифференциальное исчисление функции одной переменной.
Основные определения.
Опр. 1. Дифференцированием функции называется операция нахождения производной от функции.
Опр. 2. Производной функции y=f(x) по аргументу x называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю произвольным образом.
f ’(x)= 
Замечание: В школе считалось, что производная существует, если этот предел конечен, однако, если lim= 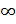 , то функция f(x) имеет в точке x бесконечную производную.
, то функция f(x) имеет в точке x бесконечную производную.
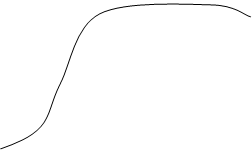
Геометрический смысл:
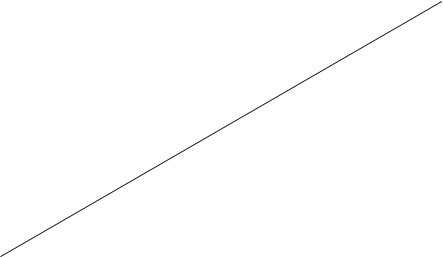 Значение производной f ’(x) при заданном значении аргумента x равно тангенсу угла, образованного с положительным направлении оси Ox касательной к графику функции f(x) в точке M0(x0,y0).
Значение производной f ’(x) при заданном значении аргумента x равно тангенсу угла, образованного с положительным направлении оси Ox касательной к графику функции f(x) в точке M0(x0,y0).
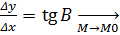 tg
tg 










 y
y
 |

Механический смысл:
Если зависимость расстояния S движущейся точки от времени t выражается формулой S=f(t), то мгновенная (не путать со средней) скорость в момент времени t выражается формулой:
v=S’(t)= 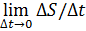 =
= 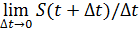 ,
,
т.е. скорость равна производной по пути от времени.
Замечание: Экономический смысл производной будет рассмотрен в отедльном параграфе.
Односторонние производные.
Опр. 1: Односторонней производной функции f(x) по аргументу x называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю слева (левосторонняя) или справа (правосторонняя), т.е.

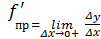
Замечания:
1) Если 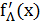 =
= 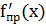 , то
, то 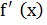 существует. В противном случае
существует. В противном случае 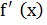 не существует.
не существует.
Пример: y=|x-1|
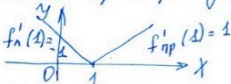
x=1 называется угловой точкой.
2) Рассмотрим случаи бесконечных односторонних производных
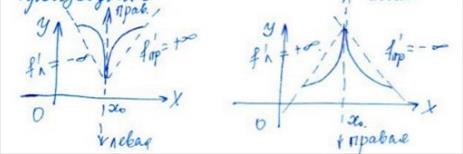
Таблица производных.

Пример: Вычислить производную функции f(x)=1/ 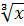 – lnx*cosx+tgx/x^7 +5sinx*5.
– lnx*cosx+tgx/x^7 +5sinx*5.
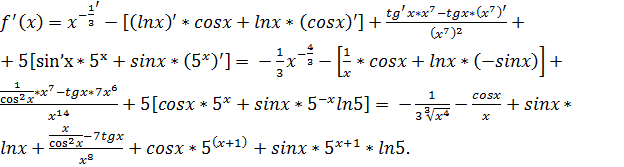
Связь между дифференцируемостью и непрерывностью.
Теорема: Если функция f(x) дифференцируема в (.) x0, то она в этой точке непрерывна.
Док-во:
Если 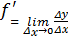 , тогда по теореме о пределе
, тогда по теореме о пределе 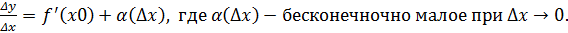
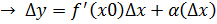
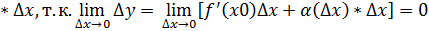
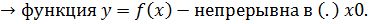
Производная сложной функции.
Теорема: Пусть дана функция y=f(x) такая, что её можно представить в виде y=F(u), г= 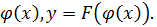 Тогда, если y=F(u) и u=
Тогда, если y=F(u) и u= 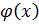 имеют производные в некоторые точки u т (.) x, то функция
имеют производные в некоторые точки u т (.) x, то функция 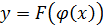 имеет в (.) x производную, которая равна
имеет в (.) x производную, которая равна
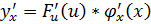
Или кратко 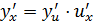 .
.
То есть производная сложной функции равна произведению производной данной функции по промежуточному аргументу «и» на производную промежуточного аргумента по x.
Доказательство:
Зададим аргументу x приращение  , тогда функция получит приращение
, тогда функция получит приращение  и
и 
Таким образом, приращению  соответствует приращение
соответствует приращение  , которое соответствует приращению
, которое соответствует приращению  , которое соответствует приращению
, которое соответствует приращению 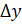 , причём при
, причём при 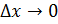 будет
будет 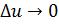 и
и 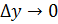 .
.
По условию  по определению предела
по определению предела 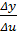 =
= 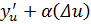 , где
, где 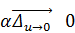 .
.
 .
.
Разделим все члены равенства 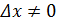 .
.
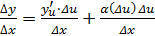 , и
, и
 |
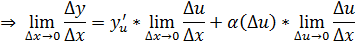

 |
 - по определению производной.
- по определению производной.
Отсюда
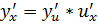 ч.т.д.
ч.т.д.
 Пример:
Пример: 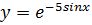
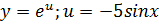

 2020-09-24
2020-09-24 116
116







