Пусть задана функция y=f(x), тогда обратная её функция будет иметь вид x= 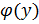 .
.
Замечания:
1. Возрастающая или убывающая функции имеют одну обратную функцию.
2. Если возрастающая или убывающая функция y=f(x) непрерывна на [a;b], причём f(a)=c; f(b)=d, тогда обратная функция будет определена и непрерывна на [c;d].
Пример:
y=sinx, x 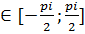
x=arcsiny, y 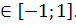
3. Если функция не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
4. Графики обратных функций будут симметричны относительно биссектрисы координат угла или совпадать.
Теорема: Если для функции y=f(x) существует обратная функция x= 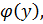 которая в рассматриваемой точке имеет производную
которая в рассматриваемой точке имеет производную 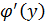 , отличную от нуля, то в этой точке функция y=f(x) имеет производную
, отличную от нуля, то в этой точке функция y=f(x) имеет производную 

Доказательство: I способ
Пусть аргумент y имеет приращение 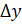 , тогда функция x получит приращение
, тогда функция x получит приращение
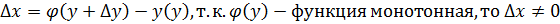
Напишем тождество:
(1) 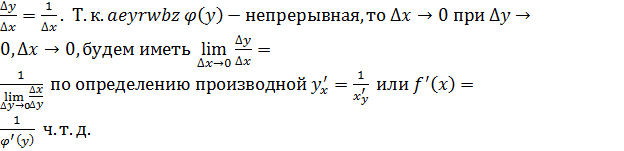
II способ
Т.к. x= 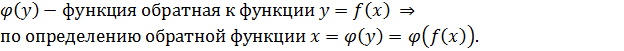

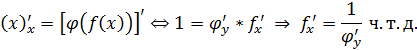
Пример: 1) Пусть y=arcsinx. Докажем, что 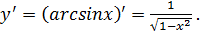
3) y=arctgx; 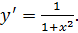
Дифференцирование сложной показательной функции.
Опр. 1. Функция вида 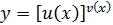 называется сложной показательной функцией [показательно-степенной или степенно-показательной].
называется сложной показательной функцией [показательно-степенной или степенно-показательной].
Теорема:
Если 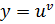 , то
, то
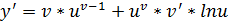
Доказательство: (логарифмическое дифференцирование)
Пусть 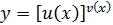 (2)
(2)
Прологарифмируем обе части равенства 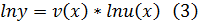
Продифференцируем обе части равенства (3) по аргументу x:
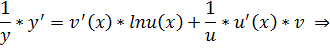
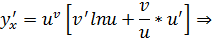
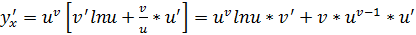 ч.т.д.
ч.т.д.
Пример: 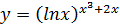
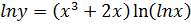
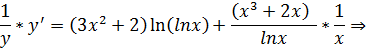
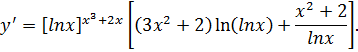
Дифференциал.
Пусть функция y=f(x) дифференцируема на отрезке [a;b], где 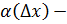 б/м при
б/м при 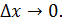
Умножим обе части последнего равенства 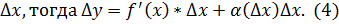
Приращение функции состоит из 2 слагаемых, одно из которых 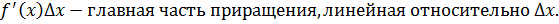
Опр. 1. Главная часть приращения функции называется дифференциалом функции и обозначается dy или df(x)

т.е. dy – произведение производной функции на приращение аргумента.
Опр. 2. Дифференциал независимого переменного x dx совпадает с его приращением 
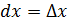
тогда определение 1 можно записать в виде
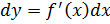
Т.о., производную функции можно рассмотреть как отношение дифференциала функции к дифференциалу независимого переменного.
Рассмотрим (4), подставив значение дифференциала
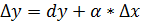
Т.о., приращение функции отличается от дифференциала функции на величину б/малую высшего порядка относительно 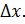
Можно показать, что если 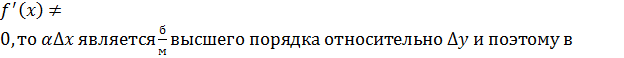
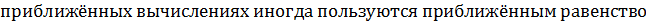
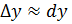
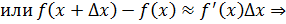
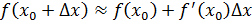
Задача нахождения дифференциала равносильна нахождению производной, т.к., умножив последнюю на дифференциал аргумента, получим дифференциал функции. Поэтому большинство теорем и формул, относящихся к производным, сохраняют свою силу и для дифференциалов.
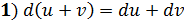
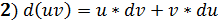
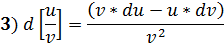
Пример: 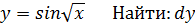
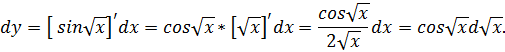
 2020-09-24
2020-09-24 85
85








