1) Вычислить определитель матрицы А. Если определитель равен нулю, то обратной матрицы не существует.
2) Если определитель матрицы не равен нулю, то составить из алгебраических дополнений соответствующих элементов матрицы А матрицу 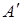 .
.
3) Транспонируя матрицу 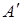 , получить присоединенную матрицу
, получить присоединенную матрицу 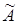 .
.
4) По формуле (2) составить обратную матрицу 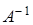 .
.
5) По формуле (1) проверить вычисления.
Пример. Найти обратную матрицу.
а). Пусть А= 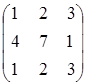 . Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
. Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
б). Пусть А = 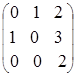 .
.
Вычислим определитель матрицы
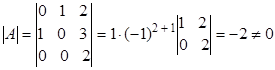
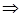 обратная матрица существует.
обратная матрица существует.
Составим матрицу из алгебраических дополнений
 =
= 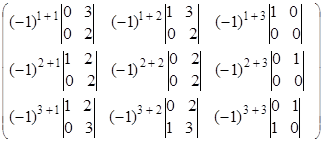 =
= 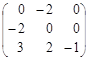 ;
;
транспонируя матрицу 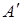 , получим присоединенную матрицу
, получим присоединенную матрицу 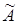
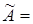
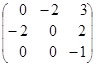 ;
;
по формуле (2) найдем обратную матрицу 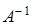
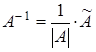 =
= 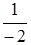
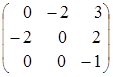 =
=  .
.
Проверим правильность вычислений
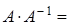
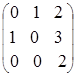
 =
=
= 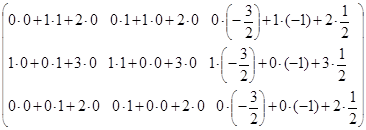 =
= 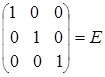 .
.
Следовательно, обратная матрица построена верна.
4. ЗАДАЧИ И УПРАЖНЕНИЯ 
4.1 Матрицы и действия над ними
1. Найти сумму, разность, произведения двух матриц А и В.
а) 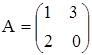 ,
, 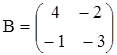 ;
;
б) 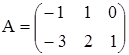 ,
, 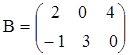 ;
;
в) 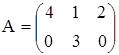 ,
, 
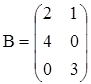 ;
;
 2020-09-24
2020-09-24 119
119







