2020-09-24
141
Задачи для самостоятельного решения (оформляются как контрольная работа)
2.1.1. Найти эмпирическую функцию по данному распределению выборки:
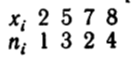
2.1.2. Построить гистограмму относительных частот по данному распределению выборки:
| Номер | Частичный интервал
| Сумма частот вариант частичного интервала 
|
| 1 | 10 – 15 | 2 |
| 2 | 15 – 20 | 4 |
| 3 | 20 – 25 | 8 |
| 4 | 25 – 30 | 4 |
| 5 | 30 – 35 | 2 |
2.2. Из генеральной совокупности извлечена выборка объема n = 60.
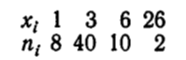
Найти несмещенную оценку генеральной совокупности.
2.3. Случайная величина Х (число появлений события А в m независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром р. Ниже приведено эмпирическое распределение числа появлений события А в 1000 испытаний (в первой строке указано число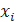 
появлений события в одном опыте из m = 10 испытаний, во второй строке приведена частота 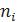– число опытов, в которых наблюдалось 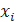появлений события А):
Найти методом наибольшего правдоподобия точечную оценку неизвестного параметра р биномиального распределения.
2.4. На обувной фабрике изготавливают детские сапоги одного размера. По выборке объема 
вычислена выборочная средняя длин подошвы сапог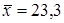 
. Найти с надежностью 0,99 доверительный интервал для средней длины 
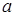подошвы сапога, если известно, что среднее квадратическое отклонение длин равно 
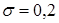. Предполагается, что длины подошв распределены нормально.
2.5. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности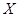 
с эмпирическим распределением выборки.
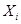
| 110 | 120 | 130 | 140 | 150 | 160 | 170 |
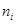
| 1 | 13 | 29 | 42 | 22 | 12 | 1 |
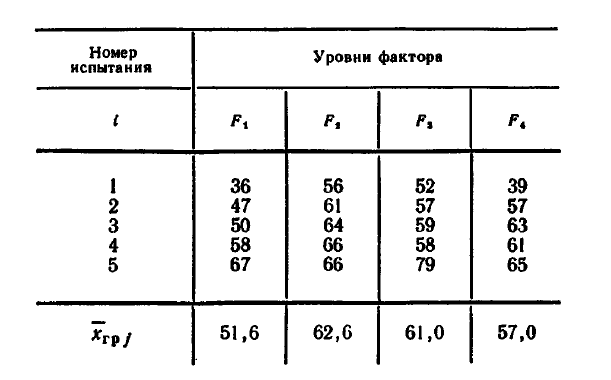
2.6. Произведено по пять испытаний на каждом из четырех уровней фактора F. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних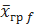 
. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Результаты испытаний приведены в таблице:
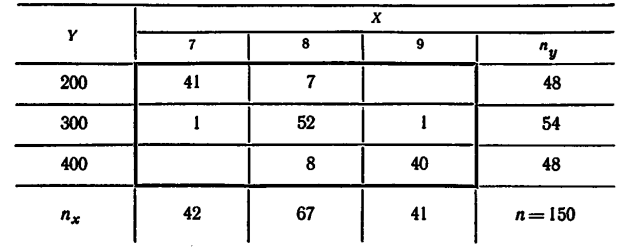
2.7. Найти выборочные уравнения прямых линий регрессии Y на X и X на Y по данным, приведенным в следующих корреляционных таблицах:
а)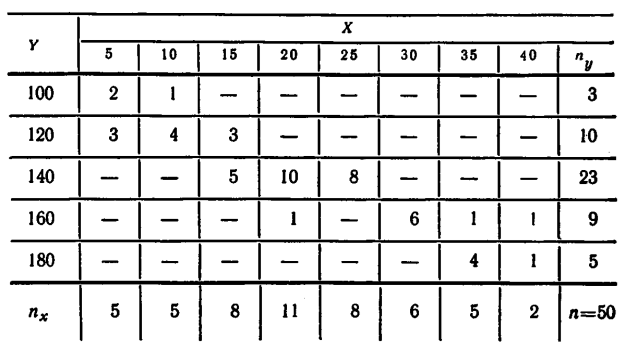 
б)
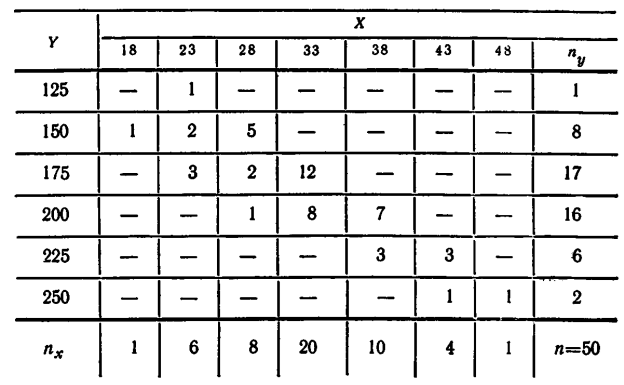
в) 
2.8. Найти выборочное уравнение регрессии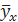 
= A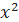 
+ Bx + C и выборочное корреляционное отношение 
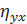по данным, приведенным в корреляционной таблице:
а)
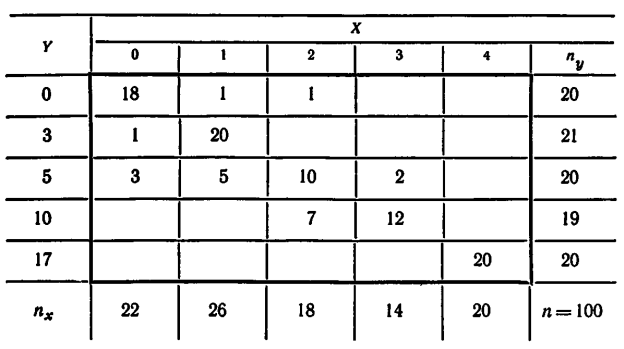
б)
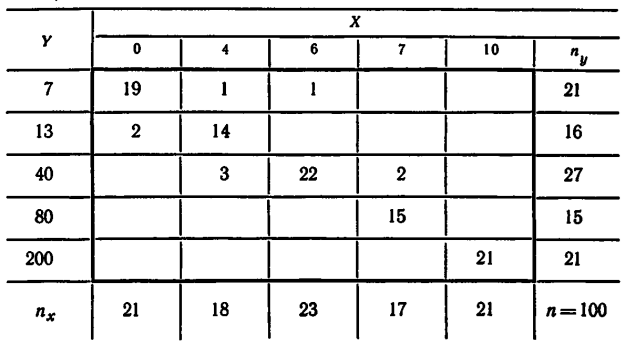
в)
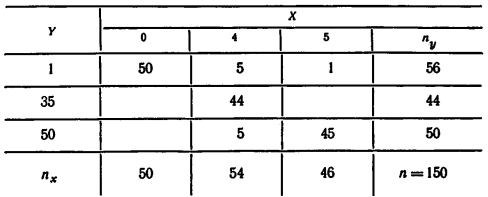
г)
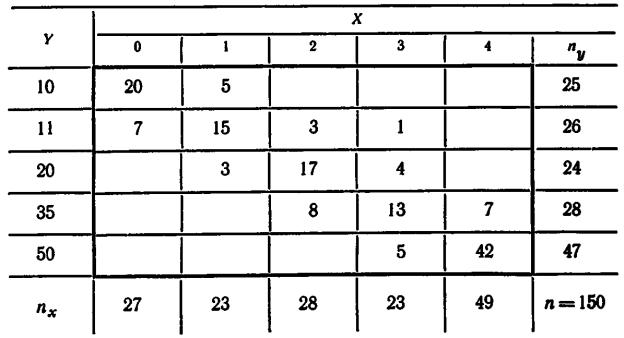
д)
Рефераты
Темы рефератов
1. Возникновение и развитие теории вероятностей.
2. Элементы комбинаторики (перестановки, размещения, сочетания).
3. Случайные события и операции над ними.
4. Классическое определение вероятности.
5. Формула Байеса.
6. Формула Бернулли.
7. Локальная и интегральная теоремы Муавра-Лапласа.
8. Теорема Пуассона.
9. Предмет и задачи математической статистики.
10. Графическое изображение вариационных рядов.
11. Эмпирическая функция распределения.
12. Интервальное оценивание.
13. Статистические гипотезы и критерии для их проверки (Критерий Пирсона. Критерий Колмогорова).
14. Критерии согласия Пирсона.
15. Элементы дисперсионного анализа.
16. Основы теории корреляции.
17. Статистика многомерных данных.
