Постановка задачі
математичний кореляційний одномірний відгук
Задана нелінійна безінерційна система, характеристики якої не залежать від часу. Математичною моделлю системи є оператор  , який називається амплітудною характеристикою системи. На вхід системи подається стаціонарний випадковий процес
, який називається амплітудною характеристикою системи. На вхід системи подається стаціонарний випадковий процес 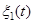 (вплив), що має гауссівський розподіл миттєвих значень з параметрами
(вплив), що має гауссівський розподіл миттєвих значень з параметрами  . Вихідним є процес
. Вихідним є процес 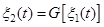 , що називається відгуком системи (рис 1.1), який є стаціонарним випадковим процесом.
, що називається відгуком системи (рис 1.1), який є стаціонарним випадковим процесом.

Рис 1.1.
Треба побудувати графіки можливих реалізацій вхідного та вихідного процесів, знайти одномірну функцію розподілу відгуку, його математичне сподівання, кореляційну функцію та проаналізувати отримані результати і зробити висновки.
Побудова графіків реалізацій вхідного та вихідного процесів
Оскільки система безінерційна, то миттєве значення вихідного процесу 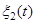 в довільний фіксований момент часу
в довільний фіксований момент часу 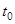 визначається значенням вхідного процесу
визначається значенням вхідного процесу 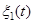 в той же момент часу:
в той же момент часу:
 (2.1)
(2.1)
Визначимо діапазон практично можливих миттєвих значень вхідного процесу 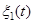 , для яких виконується умова:
, для яких виконується умова:
 (2.2)
(2.2)
Якщо вхідним є гауссівський стаціонарний випадковий процес, то для нього використовується правило «трьох 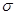 »:
»:
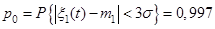 (2.3)
(2.3)
Згідно з (1.3) діапазон практично можливих значень:
 (2.4)
(2.4)
Знайдемо діапазон практично можливих значень для заданих трьох значень математичного сподівання:
1) 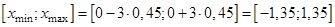 ;
;
2) 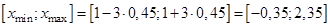 ;
;
3)  .
.
Вхідний процес отримаємо використовуючи таблицю чисел стандартної гауссівської випадкової величини. Для приведення стандартної гауссівської випадкової величини до випадкової гауссівської величини з необхідним математичним сподіванням і середньоквадратичним відхиленням використаємо формулу:
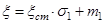 (2.5)
(2.5)
Для заданих трьох значень математичного сподівання розрахуємо 30 значень випадкової величини і розташуємо їх на вісі часу з кроком 0,1 секунда. Таким чином отримаємо три варіанти реалізації вхідного випадкового процесу.
Використовуючи відомий оператор системи 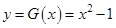 , побудуємо графіки реалізацій вхідного (
, побудуємо графіки реалізацій вхідного (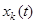 ) і вихідного (
) і вихідного (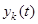 ) процесів.
) процесів.
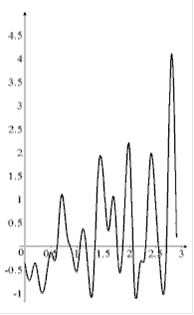
1) 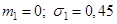
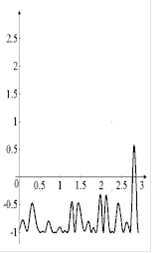

Діапазон можливих значень вихідного процесу:

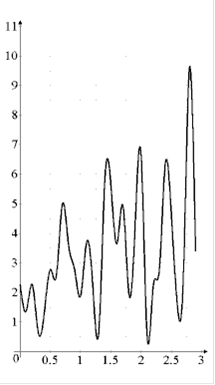
2) 



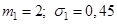
 2020-09-24
2020-09-24 78
78







