За умовою вхідний процес є гауссівським випадковим процесом, тобто його функція розподілу визначається через функцію Лапласа за формулою:
 (3.1)
(3.1)
Для заданих значень математично сподівання і середньоквадратичного відхилення знайдемо функції розподілу і побудуємо графіки:
1) 

2) 

3) 
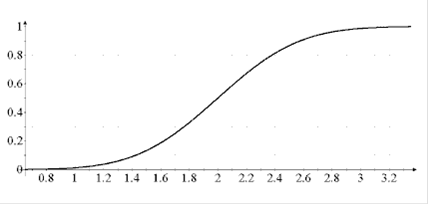
Знайдемо функцію розподілу вихідного процесу  . Для заданої системи
. Для заданої системи 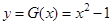 зворотною функцією є
зворотною функцією є  . Аналізуючи амплітудну характеристику системи (рис. 3.4) розглянемо два інтервали для
. Аналізуючи амплітудну характеристику системи (рис. 3.4) розглянемо два інтервали для 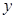 :
:
) При  :
:  .
.
) При 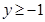 :
: 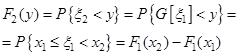 ,
,
де 
Тобто на цьому інтервалі функція розподілу має вигляд:
 (3.2)
(3.2)
Остаточний вигляд для функції розподілу вихідного процесу:
 (3.3)
(3.3)
Для заданих значень математичного сподівання і середньоквадратичного відхилення запишемо функції розподілу та побудуємо графіки:
1) 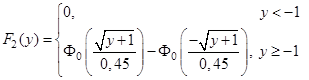

2) 
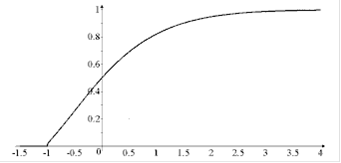
3) 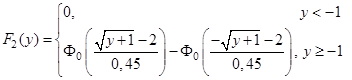

Розрахунок математичного сподівання вихідного процесу
Математичне сподівання вихідного процесу:
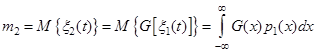 (4.1)
(4.1)
Для гауссівського вхідного процесу:
 (4.2)
(4.2)
Підставивши (4.2) в (4.1) отримаємо:
 . Введемо заміну:
. Введемо заміну:
 . Тоді:
. Тоді:

Для знаходження інтегралів скористаємося відомим співвідношенням:
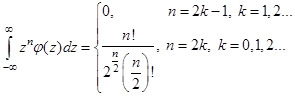 (4.3)
(4.3)

Обчислимо значення математичного сподівання вихідного процесу для трьох значень математичного сподівання вхідного процесу:
  
| ||
| 0,45 | 0 | -0,7975 |
| 1 | 0,2025 | |
| 2 | 3,2025 |
Розрахунок кореляційної функції вихідного процесу
Для знаходження кореляційної функції вихідного процесу використаємо формулу:
 , (5.1)
, (5.1)
де 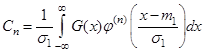 , а
, а  , за умовою.
, за умовою.
Визначимо перші три коефіцієнта розкладу кореляційної функції в ряд. Для цього введемо заміну:
 .
.
1) 
Відомо, що  . Тоді:
. Тоді:
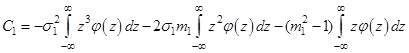
Використовуючи (4.3) отримаємо:
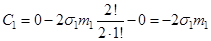
2) 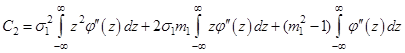
Відомо, що  . Тоді:
. Тоді:

3) 
Відомо, що 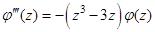 . Тоді:
. Тоді:


Наближені вирази для кореляційної функції та її графіки для трьох значень математичного сподівання:
1) 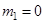 :
: 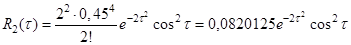
 :
: 

2) 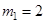 :
: 
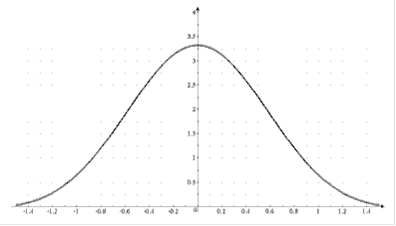
Висновки
Розраховані практично можливі значення для вхідного і вихідного процесів для трьох значень математичного сподівання:
  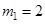
| |||
 [-1,35; 1,35][-0,35; 2,35][0,65; 3,35] [-1,35; 1,35][-0,35; 2,35][0,65; 3,35]
| |||
 [-1; 0,8225][-1; 4,5225][-0,5775; 10,2225] [-1; 0,8225][-1; 4,5225][-0,5775; 10,2225]
|
Отриманий загальний вираз для функції розподілу вихідного процесу:

Вираз для обчислення математичного сподівання вихідного процесу:
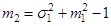
Визначені значення для математичного сподівання вихідного процесу для трьох значень математичного сподівання вхідного процесу:
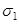 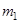 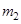
| ||
| 0,45 | 0 | -0,7975 |
| 1 | 0,2025 | |
| 2 | 3,2025 |
Отримані вирази для перших трьох коефіцієнтів розкладу кореляційної функції вихідного процесу в ряд:
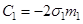 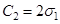 
|
Наближені вирази для кореляційної функції вихідного процесу для трьох значень математичного сподівання вхідного процесу:
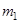 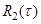
| |
| 0 | 
|
| 1 | 
|
| 2 | 
|
Література
1. Аналіз нелінійного перетворення стаціонарного гауссівського випадкового процесу. Методичні рекомендації до виконання курсової роботи з дисципліни «Теорія процесів та систем. Випадкові процеси» для студентів напрямку підготовки 050803 - Акустотехніка / Уклад.: О. В. Гармаш, Т. А. Горовецька, О. І. Красильніков. - К.: ВЦ «Принт-центр», 2008. - 44 с.
2. Тихонов В. И. Статистическая радиотехника. - М.: Сов. Радио, 1982. - 624 с.
. Гнеденко Б. В. Курс теории вероятностей: Учебник. - М.: Едиториал УРСС, 2005. - 448 с.
. Левин Б. Р. Теоретические основы статистической радиотехники. - М.: Сов. Радио, 1974. - 552 с.
 2020-09-24
2020-09-24 89
89







