Оценка финансовых рисков

 

При принятии того или иного решения, финансовые менеджеры всегда рискуют, поскольку нельзя исключить возможность нежелательных событий. Но можно сократить вероятность их появления и возможный ущерб. Для этого необходимо спрогнозировать дальнейшее развитие событий, в частности, последствия принимаемых решений, выявить риски, оценить их, а затем управлять рисками. Это и есть основные задачи риск-менеджмента.

Теоретической основой методов прогнозирования являются математические дисциплины (прежде всего, теория вероятностей и математическая статистика, дискретная математика, исследование операций), а также экономическая теория, экономическая статистика, менеджмент, социология, политология и другие социально-экономические науки.

Как общепринято со времен основоположника научного менеджмента Анри Файоля, прогнозирование и планирование - основа работы менеджера. Сущность эконометрического прогнозирования состоит в описании и анализе будущего развития, в отличие от планирования, при котором директивным образом задается будущее движение.

Часто оказывается полезным промежуточный путь между прогнозированием и планированием - так называемое нормативное прогнозирование. При его применении сначала задается цель (т.е. «норма», которой необходимо следовать), затем разрабатывается система мероприятий, обеспечивающая достижение этой цели, и изучаются характеристики этой системы (объем необходимых ресурсов, в том числе материальных, кадровых, финансовых, временных, возникающие риски и т.п.).

Прогнозирование на основе данных, имеющих нечисловую природу, в частности, прогнозирование качественных признаков основано на результатах статистики нечисловых данных. Весьма перспективными для прогнозирования представляются регрессионный анализ на основе интервальных данных, включающий, а также регрессионный анализ нечетких данных, разработанный в монографии - первой книге российского автора по нечетким множествам. Общая постановка регрессионного анализа в рамках статистики нечисловых данных и ее частные случаи - дисперсионный анализ и дискриминантный анализ (распознавание образов с учителем) дает единый подход к формально различным методам, традиционно рассматриваемым как принципиально различные. Она полезна при программной реализации современных статистических методов прогнозирования.

Необходимость и общее представление о применении экспертных методов прогнозирования при принятии решений на различных уровнях управления - на уровне страны, отрасли, региона, предприятия. Отметим большое практическое значение экспертиз при сравнении и выборе инвестиционных и инновационных проектов, при управлении проектами, экологических экспертиз. Роли лиц, принимающих решения, и специалистов (экспертов) в процедурах принятия решений, критерии принятия решений и место экспертных оценок в процедурах принятия решений рассматриваются в экспертологии - научно-практической дисциплине, посвященной методам экспертных оценок. На ее основе формируются конкретные процедуры подготовки и принятия решений с использованием методов экспертных оценок, например, процедуры распределения финансирования научно-исследовательских работ (на основе балльных оценок или парных сравнений), технико-экономического анализа, кабинетных маркетинговых исследований (противопоставляемых «полевым» выборочным исследованиям), оценки, сравнения и выбора инвестиционных проектов. При прогнозировании широко используются такие методы, как метод Дельфи, метод «мозгового штурма» и метод сценариев.

В конкретных задачах прогнозирования необходимо провести классификацию рисков, поставить задачу оценивания конкретного риска, провести структуризацию риска, в частности, построить деревья причин (в другой терминологии, деревья отказов) и деревья последствий (деревья событий). Центральной задачей является построение групповых и обобщенных показателей, например, показателей конкурентоспособности и качества. Риски необходимо учитывать при прогнозировании экономических последствий принимаемых решений, поведения потребителей и конкурентного окружения, внешнеэкономических условий и макроэкономического развития России, экологического состояния окружающей среды, безопасности технологий, экологической опасности промышленных и иных объектов. Метод сценариев незаменим применительно к анализу технических, экономических и социальных последствий аварий.

Имеется некоторая специфика применения методов прогнозирования в ситуациях, связанных с риском. Велика роль функции потерь и методов ее оценивания, в том числе в экономических терминах. В конкретных областях используют вероятностный анализ безопасности (для атомной энергетики) и другие специальные методы.

Методический инструментарий оценки уровня финансового риска является наиболее обширным, так как включает в себя разнообразные экономико-статистические, экспертные, количественные и качественные методы осуществления такой оценки. Выбор конкретных методов оценки определяется наличием необходимой информационной базы и уровнем квалификации менеджеров.

Одним из наиболее распространенных методов оценки финансового риска является «лемма Маркова». Лемма Маркова гласит: если случайная величина Х не принимает отрицательных значений, то для любого положительного числа α справедливо следующее неравенство:

 

Р (Х > α) ≤ М (х) / α, (1)

 

где М (х) - математическое ожидание, то есть среднее значение случайной величины;

Х - любая случайная величина.

К другим широко используемым методам относят:

Неравенство Чебышева:

 

Р (|х - х| > ε) ≤ σ²/ε². (2)

 

Оно позволяет находить верхнюю границу вероятности того, что случайная величина Х отклонится в обе стороны от своего среднего значения на величину больше ε.

Эта вероятность равна или меньше (как максимум равна, не больше), чем σ²/ε², где σ² - дисперсия, исчисляемая по формуле:

 

σ² = Σ (х - х)² / n. (3)

 

Если нас интересует вероятность отклонения только в одну сторону, например, в большую, то вышеприведенное неравенство Чебышева надо было бы записать так:

 

Р ((х - х) > ε) ≤ σ² / (ε²*2). (4)

 

Неравенство Чебышева дает значение вероятности отличное от значения, полученного решая лемму Маркова. Это объясняется тем, что неравенство Чебышева кроме среднего уровня показателей учитывает и еще его колеблемость.

Лемма Маркова и неравенство Чебышева пригодны для употребления при любом количестве наблюдений и любом законе распределения вероятностей. Это является их большим достоинством. Платой за отсутствие жестких ограничений является некоторая неопределенность оценок уровня вероятности, причем при использовании леммы Маркова она значительно больше, чем при применении неравенства Чебышева.

Неопределенность оценок существенно снижается, если можно допустить наличие закона нормального распределения. Как известно, условия существования этого закона довольно широки, что позволяет допускать его наличие в очень многих случаях.

Многообразие показателей, посредством которых осуществляется количественная оценка, порождает и многообразие шкал риска являющихся своего рода рекомендациями приемлемости того или иного уровня риска. На основании обобщения результатов исследований многих авторов по проблеме количественной оценки риска ниже приведена эмпирическая шкала риска, которую рекомендуют применять предпринимателям при использовании ими в качестве количественной оценки риска вероятности наступления рискового события.

 

Таблица 2 Шкалы риска

Величина риска	Наименование градаций риска
0,0-0,1	минимальный
0,1-0,3	малый
0,3-0,4	средний
0,4-0,6	высокий
0,6-0,8	максимальный
0,8-1,0	критический

 

Первые три градации вероятности нежелательного исхода соответствуют «нормальному», «разумному» риску, при котором рекомендуется принимать обычные предпринимательские решения. Принятие решений с большим риском возможно, если наступление нежелательного исхода не приведет к банкротству.

Для оценки колеблемости (изменчивости) риска используется коэффициент вариации (V = σ / X) и приводятся следующие шкалы: до 0,1 - слабая; от 0,1-0,25 - умеренная; свыше 0,25 - высокая.

При оценке приемлемости коэффициента, определяющего риска банкротства существует несколько не противоречащих друг другу точек зрения. Одни авторы считают, что оптимальным является коэффициент риска, составляющий 0,3, а коэффициент риска, ведущий к банкротству - 0,7 и выше. В других источниках приводится шкала риска со следующими градациями указанного выше коэффициента: до 0,25 - приемлемый; 0,25-0,50 - допустимый; 0,50-0,75 - критический; свыше 0,75 - катастрофический риск.

Существуют описательные характеристики шкал риска по величине ожидаемых потерь, которые используются для оценки приемлемости содержащего риск решения. В этих градациях риска в зависимости от уровня возможных потерь осуществляются путем выделения следующих весьма условных зон.

. Область минимального риска характеризуется уровнем потерь, не превышающим размеры чистой прибыли.

. Область повышенного риска характеризуется уровнем потерь, не превышающим размеры расчетной прибыли.

. Область критического риска характеризуется тем, что в границах этой зоны возможны потери, величина которых превышает размеры расчетной прибыли, но не превышает размер ожидаемых доходов.

. Область недопустимого риска характеризуется тем, что в границах этой зоны ожидаемые потери способны превзойти размер ожидаемых доходов от операции и достичь величины, равной всему имущественному состоянию предпринимателя.

Отмеченный подход, разработанный в 1968 г. Эдвардом Альтманом, был применен им самим в том же году применительно к экономике США. В результате появилось широко известная формула:

 

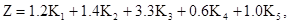                       (5)

 

где К₁ = собственный оборотный капитал / сумма активов;

К₂ = нераспределенная прибыль / сумма активов;

К₃ = прибыль до уплаты процентов / сумма активов;

К₄ = рыночная стоимость собственного капитала / заемный капитал;

К₅ = объем продаж / сумма активов.

Интервальная оценка Альтмана: при Z<1.81 - высокая вероятность банкротства, при Z>2.67 - низкая вероятность банкротства.

Сопоставление данных, полученных для ряда стран, показывает, что веса в Z - свертке и пороговый интервал [Z1, Z2] сильно разнятся не только от страны к стране, но и от года к году в рамках одной страны (можно сопоставить выводы Альтмана о положении предприятий США за 10 лет анализа). Получается, что подход Альтмана не обладает устойчивостью к вариациям в исходных данных. Статистика, на которую опирается Альтман и его последователи, возможно, и репрезентативна, но она не обладает важным свойством статистической однородности выборки событий. Одно дело, когда статистика применяется к выборке радиодеталей из одной произведенной партии, а другое, - когда она применяется к фирмам с различной организационно-технической спецификой, со своими уникальными рыночными нишами, стратегиями и целями, фазами жизненного цикла и т.д. Здесь невозможно говорить о статистической однородности событий, и, следовательно, допустимость применения вероятностных методов, самого термина «вероятность банкротства» ставится под сомнение.

Но ключевым ограничением этого метода является даже не проблема качественной статистики. Дело в том, что классическая вероятность - это характеристика не отдельного объекта или события, а характеристика генеральной совокупности событий. Рассматривая отдельное предприятие, мы вероятностно описываем его отношение к полной группе. Но уникальность всякого предприятия в том, что оно может выжить и при очень слабых шансах, и, разумеется, наоборот. Единичность судьбы предприятия подталкивает исследователя присмотреться к предприятию пристальнее, расшифровать его уникальность, его специфику, а не «стричь под одну гребенку»; не искать похожести, а, напротив, диагностировать и описывать отличия. При таком подходе статистической вероятности места нет. Исследователь интуитивно это чувствует и переносит акцент с прогнозирования банкротства (которое при отсутствии полноценной статистики оборачивается гаданием на кофейной гуще) на распознавание сложившейся ситуации с определением дистанции, которая отделяет предприятие от состояния банкротства. Вследствие вышесказанного предлагается использовать метод оценки риска банкротства, разработанный отечественными экономистами Недосекиным А.О. и Максимовым О.Б.

Эксперту необходимо выбрать ряд отдельных финансовых показателей, о которых можно сказать, что они наилучшим образом характеризуют отдельные стороны деятельности предприятия и при этом образуют некую законченную совокупность, дающую исчерпывающее представление о предприятии как о целом. Выбор системы показателей для анализа - искусство, стяжаемое долгим опытом анализа. Значимость тех или иных показателей для оценки тех или иных предприятий различна, и поэтому перед экспертом встает трудная задача отбора и ранжирования факторов анализа. Показатели, классифицированные по группам (финансовая устойчивость, ликвидность, рентабельность и т.д.), могут образовывать иерархию, но в простейшем случае они просто составляют неупорядоченный набор.

Причем здесь и далее по умолчанию предполагаем, что рост отдельного показателя Х_i сопряжен со снижением степени риска банкротства и с улучшением самочувствия рассматриваемого предприятия. Если для данного показателя наблюдается противоположная тенденция, то в анализе его следует заменить сопряженным. Например, показатель доли заемных средств в активах предприятия разумно заменить показателем доли собственных средств в активах.

Пример системы показателей:

-  Х₁ - коэффициент автономии (отношение собственного капитала к валюте баланса);

-  Х₂ - коэффициент обеспеченности оборотных активов собственными средствами (отношение чистого оборотного капитала к оборотным активам);

-  Х₃ - коэффициент промежуточной ликвидности (отношение суммы денежных средств и дебиторской задолженности к краткосрочным пассивам);

-  Х₄ - коэффициент абсолютной ликвидности (отношение суммы денежных средств к краткосрочным пассивам);

-  Х₅ - оборачиваемость всех активов в годовом исчислении (отношение выручки от реализации к средней за период стоимости активов);

-  Х₆ - рентабельность всего капитала (отношение чистой прибыли к средней за период стоимости активов).

Сопоставим каждому показателю Х_i уровень его значимости для анализа r_i. Чтобы оценить этот уровень, нужно расположить все показатели по порядку убывания значимости так, чтобы выполнялось правило

 

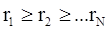.                                      (6)

 

Если система показателей проранжирована в порядке убывания их значимости, то значимость i-го показателя r_i следует определять по правилу Фишберна:

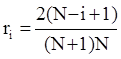.                          (7)

 

Например, для системы с N=3 показателями r₁ = 3/6, r₂ = 2/6, r₃ = 1/6, и сумма уровней значимости равна единице.               

Если все показатели обладают равной значимостью, тогда

 

r_i = 1/N.          (8)