Задача 4 (осевая симметрия)

Доказать, что из всех треугольников с данным основанием и данной высотой равнобедренный треугольник имеет наименьший периметр. [Учебным пособием являлся учебник «Геометрия» В.Г. Болтянского и И.М. Яглома, задача №37, стр.113]

Дано:

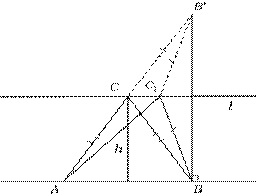
Решение:

Рассмотрим осевую симметрию с осью l║AB, BB’ 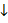 AB, f(B)=B’;расстояние от l до AB равно h. Пусть 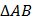C₁ – равнобедренный. 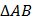C – произвольный с основанием AB и высотой h. Докажем, что.

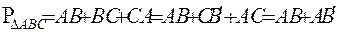
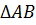Доказательство: B’ – прямоугольный треугольник, значит вокруг него можно описать окружность с центром в точке C:                                             ,           т. е.                                                                                (1)

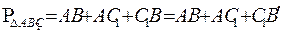                                                                . (2)

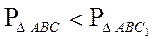 Сравнивая (1) и (2), имеем                             , т. е.                                . ч. т. д.

Задача 5 (центральная симметрия)

На сторонах параллелограмма ABCD вне его построены правильные ΔABM, ΔBCK, ΔCDP, ΔDAH. Доказать, что точки и являются вершинами параллелограмма. [Учебным пособием являлся учебник «Геометрия» В.Г. Болтянского и И.М. Яглома, задача №35, стр.109]

Дано:

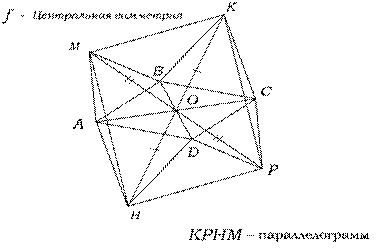
Решение:

Рассмотри центральную симметрию (поворот на 180⁰) относительно точки О. Пусть f - центральная симметрия.f(B)=D,f(A)=C,f(D)=B, f(C)=A.

 При центральной симметрии f, 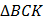(правильный) перейдет в равный ему 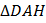(правильный), по свойствам осевой симметрии (углы сохраняются). Аналогично  переходит в .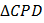

f(M)=P, f(K)=H  KO=OH, MO=OP по признаку параллелограмма, KPHM – параллелограмм.