Непосредственное интегрирование.
Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме. Пример: Вычислить ∫ (2х3 -Зх2 +2x-7)dx.
В данном примере под знаком интеграла стоит алгебраическая сумма функций. Согласно свойству 5 неопределенного интеграла,
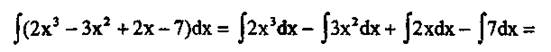
Последовательно применяя свойство 4 неопределенных интегралов и основные формулы интегрирования, получаем:
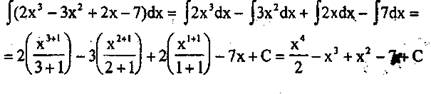
Интегрирование подстановкой (заменой переменной).
Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.
Пример: Вычислить 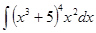
Решение: введем подстановку х3+5 = t. Продифференцируем левую часть подстановки по х, а правую по t.
(х3+5)/ dx =dt; 3x2dx = dt; следовательно х2dx = 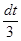 .
.
Тогда 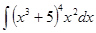 =
= 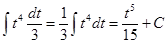 . Подставляя вместо t его значение х3+5, получим:
. Подставляя вместо t его значение х3+5, получим:
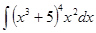 =
= 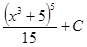
Интегрирование но частям.
Если u = u(x) vi v = v(x) - дифференцируемые функции, то фор мула интегрирования по частям имеет вид:
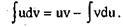 Способ интегрирования по частям применяется в том случае, когда интеграл в правой части формулы более прост для вычисления, чем исходный
Способ интегрирования по частям применяется в том случае, когда интеграл в правой части формулы более прост для вычисления, чем исходный
Пример: Вычислить 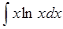
Решение: обозначим lnx через u, тогда xdx = dv. Находим:
du = d(lnx) = (lnx)/, dx = dv/x, 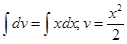
Используя формулу интегрирования по частям, получаем:
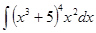 =
= 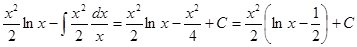
 2020-09-24
2020-09-24 384
384








