Практическая работа №7

 

Тема: Разложение функций в ряд Фурье.

Цель работы: Закрепить и систематизировать знания по теме: «Ряды».

Задание: Найдите первые четыре члена ряда по заданному члену:

1.		4.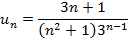
2.		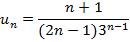5.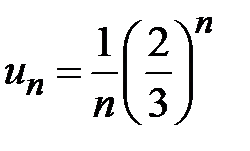
3.		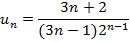6.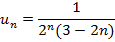

Задание: Написать простейшую формулу n -го члена ряда по указанным его первым членам и записать ряд, используя знак суммы (S):

7.		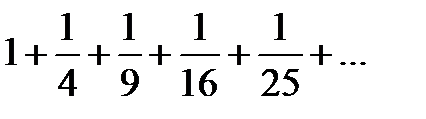10.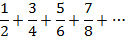
8.		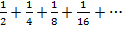11.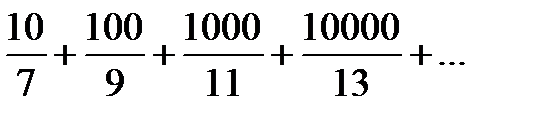
9.		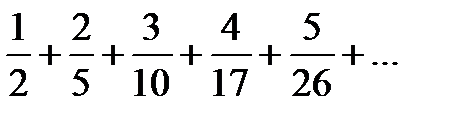12.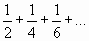

Задание: Исследовать ряд на сходимость, применяя признак Коши:

13.		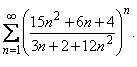16.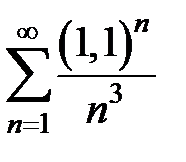
14.		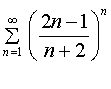17.
15.		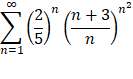18.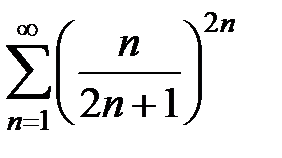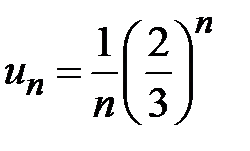

Задание: Исследовать ряд на сходимость, применяя признак Даламбера:

19.		22.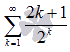
20.		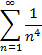23.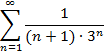
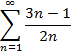
21.		24.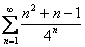

Задание: Разложите в ряд Фурье функцию:

25.		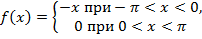28.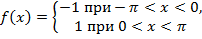
26.		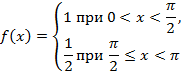29.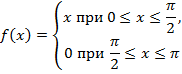
27.		30.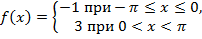

Пояснения к работе:

Необходимые формулы:

Частичная сумма ряда

Пусть 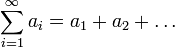— числовой ряд.

Число 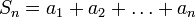 называется n-ой частичной суммой ряда.

 

Сумма (числового) ряда 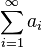— это предел частичных сумм, если он существует и конечен. Таким образом, если существует число  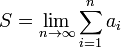 то в этом случае пишут  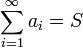. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Признак Даламбера:

Если для ряда с положительными членами 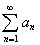существует  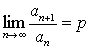, то при p<1 ряд сходится, при p>1 ряд расходится, при p=1 вопрос о сходимости остается открытым.

Разложение в ряд Фурье периодических функций Т=2L,

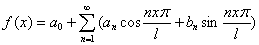
Коэффициенты Фурье

;

;

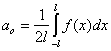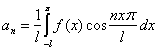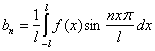 ; n = 1, 2, 3, …:;;, n = 1, 2, 3, …

Содержание отчета

1. Титульный лист в соответствии с СТП1.2-2005.

2. Цель работы

3. Задание

4. Выполненная практическая работа в соответствии с заданием

5. Ответы на контрольные вопросы

6. Вывод

Контрольные вопросы:

1. Дайте определение числового ряда.

2. Перечислите виды рядов.

3. Дайте определение понятию «сходящийся» и «расходящийся ряд.

4. Сформулируйте признак Даламбера.

5. Запишите общий вид тригонометрического ряда Фурье.