Цель работы: научиться выполнять действия над комплексными числами в алгебраической форме, решать квадратные уравнения с отрицательным дискриминантом.
1. Вычислить: 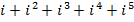
Решение: 
2. Найти x и у из равенства: 5x-2i+(y-4)i=6+3i
Решение: 5x-2i+(y-4)i=6+3i
5x-6i+yi=6+3i
5x+(y-6)i=6+3i
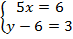
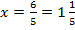
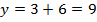
Ответ: (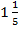 ;
; 
3. Дано: 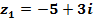
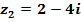
Найти: а) 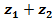 ; б)
; б) 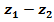 ; в)
; в) 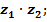 г)
г) 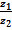 .
.
Решение:
а) 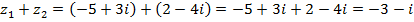
б) 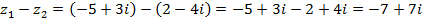
в) 
г) 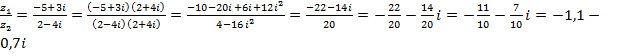
4. Выполните действия:
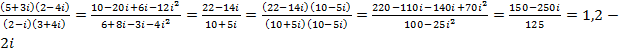
5. Решить уравнение:
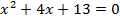
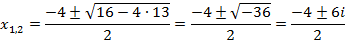
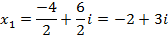
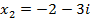
Контрольные вопросы:
Дайте определение комплексного числа
Комплексным числом z называется пара (x, y) действительных чисел x и y.
Запишите правило равенства комплексных чисел
Два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2;
Запишите правило суммы комплексных чисел.
Суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
Запишите правило деления комплексных чисел
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что 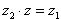 . Отсюда находим
. Отсюда находим 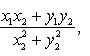
 2020-09-24
2020-09-24 115
115








