Алгоритм подвоєння-додавання-віднімання

Складність деяких методів експоненціювання точки кривої

 

Найпоширенішою операцією у всіх криптографічних алгоритмах є  - кратне додавання точки , позначуване як

Цю операцію звичайно називають скалярним множенням, або, звертаючись до термінології мультиплікативної групи, експоненціюванням точки кривої.

З метою підвищення продуктивності під час обчислення точки  багатьма авторами запропоновано різні методи. Дамо стислий опис й оцінку складності найпоширеніших з них.

Підхід до розрахунку точки  може відрізнятися залежно від того, чи є точка  фіксованою (заздалегідь відомою) або довільною точкою. У першому випадку завжди можна користуватися передрозрахунками точок, наприклад, , які зберігаються в пам'яті. Двійкове подання числа  дозволяє селектрувати ті з них, які в результаті підсумовування утворять точку . У другому, більш загальному випадку, всі обчислення доводиться проводити в реальному часі.

Нехай порядок  і число  подано у двійковій системі

 

 

Розглянемо спочатку основні алгоритми експоненціювання при невідомій заздалегідь точці

експоненціювання алгоритм скалярне множення

Алгоритм подвоєння-додавання

 

Це найприродніший і найпростіший метод, при якому обчислення здійснюються за формулою

 

 

Ці обчислення на основі методу розрахунку ліворуч-праворуч здійснюються за допомогою наступного алгоритму.

Алгоритм 1.

Вхід:

Вихід:

1.

2.

2.1

2.2

3. .

Реалізація методу вимагає  операцій  подвоєння точки й  додавань , де  - вага Хеммінга двійкового вектора  (число одиниць цього вектора). Оскільки в середньому число одиниць випадкового вектора дорівнює , загальне число групових операцій оцінюється величиною

Алгоритм подвоєння-додавання-віднімання

 

Попередній алгоритм можна вдосконалити, якщо вести додаткову операцію-віднімання точки. Цей метод запропонований в 1990 році Ф. Морейном і Дж. Олівосом. Наприклад, число  у двійковій системі має вага у , але його можна подати як  з вагою  Ця ідея знижує вагу Хеммінга і, відповідно, число групових операцій. 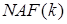Реалізувати алгоритм подвоєння - додавання віднімання можна переходом від двійкового подання числа  до трійкового  з коефіцієнтами  Одне із властивостей подання 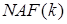 - відсутність у ньому суміжних пар ненульових елементів, завдяки чому зростає питома вага нульових елементів . 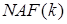Для розрахунку  використовується наступний алгоритм.

Алгоритм 2.

Вхід: позитивне ціле число

Вихід:

1.

2.

2.1

2.2

2.3

3.

Після розрахунку 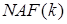 обчислюється точка  методом ліворуч-праворуч за допомогою алгоритму 3.

Алгоритм 3.

Вхід:

Вихід:

1.

2.

2.1

2.2

2.3

3. .

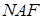-подання числа  може виявитися на один біт більше двійкового. Водночас, для випадкового  ймовірність ненульових елементів  і  знижується від  до , тобто, у середньому, для  - розрядного числа їхня кількість оцінюється величиною . Тоді загальне середнє число групових операцій додавання  й подвоєння  в алгоритмі 3 можна оцінити як суму