Фіксованою точкою в криптосистемі завжди є генератор або базова точка криптосистеми порядку  . Такі точки - це відкриті ключі користувачів. Якщо в системі є резерв пам'яті, його можна використати для зберігання заздалегідь розрахованих точок. Наприклад, якщо обчислити й записати в пам'яті точки
. Такі точки - це відкриті ключі користувачів. Якщо в системі є резерв пам'яті, його можна використати для зберігання заздалегідь розрахованих точок. Наприклад, якщо обчислити й записати в пам'яті точки  , то для визначення скалярного добутку
, то для визначення скалярного добутку 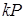 залишиться лише обчислити суми точок відповідно до двійкового подання
залишиться лише обчислити суми точок відповідно до двійкового подання 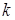 . У середньому для цього буде потрібно лише
. У середньому для цього буде потрібно лише 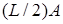 операцій. Їхнє число можна зменшити до
операцій. Їхнє число можна зменшити до 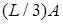 операцій додавання й віднімання, якщо скористатися трійковим поданням
операцій додавання й віднімання, якщо скористатися трійковим поданням 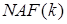 .
.
Другим досить витонченим підходом є підхід на основі вікон з фіксованою базою. Замість двійкового подання числа використовується 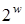 -е із передобчислюванням точок
-е із передобчислюванням точок 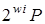 . Дійсно, нехай
. Дійсно, нехай 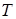 -е подання числа
-е подання числа 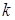 має вигляд
має вигляд

Тоді
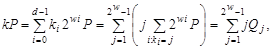
де 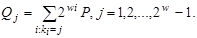
Ці обчислення здійснюються за допомогою наступного алгоритму.
Алгоритм 6.
Вхід: ширина вікна 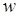 ,
, 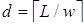 ,
, 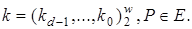
Вихід: 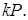
1. Передрозрахунки: 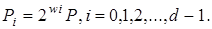
2. 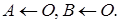
3. 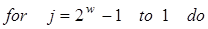
3.1 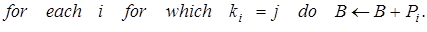
3.2 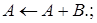
4. 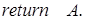
Середня обчислювальна складність алгоритму оцінюється кількістю додавань:
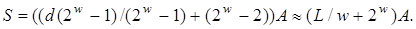 .
.
Метод вікон у цьому випадку більше продуктивний, ніж при невідомій точці, тому що передрозрахунки не входять в алгоритм експоненціювання. Якщо використати поряд з додаванням подвоєння точки, реалізувати алгоритм можна інакше. Два вікна точки 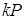 шириною
шириною 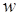 кожне можна подати у вигляді:
кожне можна подати у вигляді:

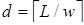 ;
;
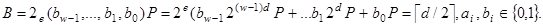
Всі можливі точки 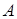 й
й 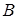 обчислюються на етапі передрозрахунків і записуються на згадку. Загальна кількість цих точок
обчислюються на етапі передрозрахунків і записуються на згадку. Загальна кількість цих точок 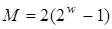 зростає експоненційно зі збільшенням ширини вікна
зростає експоненційно зі збільшенням ширини вікна 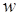 . Двійкове подання точки
. Двійкове подання точки 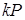 розбивається далі на
розбивається далі на 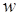 фрагментів шириною
фрагментів шириною 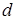 . У кожному такому фрагменті відбираються старші розряди й розряди зі зрушенням вправо на
. У кожному такому фрагменті відбираються старші розряди й розряди зі зрушенням вправо на 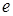 (тобто на половину фрагмента).
(тобто на половину фрагмента).
Їхні двійкові подання дають першу пару точок 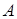 й
й 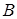 , які складаються, після чого їхня сума подвоюється.
, які складаються, після чого їхня сума подвоюється.
Далі реалізується алгоритм послідовних додавань і подвоєнь праворуч із двома вікнами, описаний нижче.
Алгоритм 7.
Вхід: ширина вікна 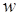 ,
, 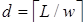 ,
, 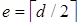 ,
, 
Вихід: 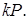
1. Передрозрахунки: обчислити всі точки  й
й
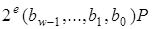 ,
, 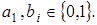
2. Подати число 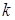 у вигляді конкатенації фрагментів шириною
у вигляді конкатенації фрагментів шириною 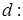
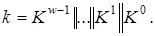 Нехай
Нехай 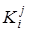 означає
означає 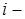 й біт фрагмента
й біт фрагмента 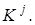
3. 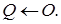
4. 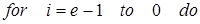
4.1 
4.2 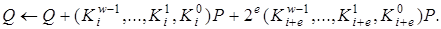
5. 
Обчислювальна складність цього алгоритму оцінюється числом групових операцій
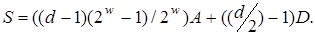
Обмінюючи час обчислень на пам'ять, можна й далі підвищувати продуктивність експоненціювання точки кривої. Наприклад, для кожного вікна шириною 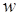 можна заздалегідь розрахувати
можна заздалегідь розрахувати 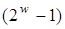 точок, при цьому на згадку рийдеться записати
точок, при цьому на згадку рийдеться записати 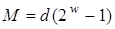 точок. Операція подвоєння в цьому випадку не використовується, а складність оцінюється числом
точок. Операція подвоєння в цьому випадку не використовується, а складність оцінюється числом 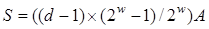 додавань. Цей алгоритм назвемо алгоритмом максимальної пам'яті. У табл.13.1 дані для порівняння величини пам'яті
додавань. Цей алгоритм назвемо алгоритмом максимальної пам'яті. У табл.13.1 дані для порівняння величини пам'яті 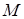 й тимчасової складності
й тимчасової складності 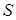 (числа групових операцій) алгоритму 6 й алгоритму максимальної пам'яті при
(числа групових операцій) алгоритму 6 й алгоритму максимальної пам'яті при 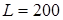 . В обох випадках зі збільшенням ширини вікна збільшується пам'ять і знижується число групових операцій. Очевидно, що останній алгоритм за наявності більших резервів пам'яті дозволяє істотно прискорити операцію експоненціювання фіксованої точки
. В обох випадках зі збільшенням ширини вікна збільшується пам'ять і знижується число групових операцій. Очевидно, що останній алгоритм за наявності більших резервів пам'яті дозволяє істотно прискорити операцію експоненціювання фіксованої точки 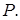
Таблиця 1 - Об'єм пам'яті 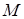 й тимчасова складність
й тимчасова складність 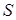 (число групових операцій) алгоритму 6 й алгоритму максимальної пам'яті при
(число групових операцій) алгоритму 6 й алгоритму максимальної пам'яті при 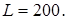
| Метод | W = 3 | W = 4 | W = 5 | W = 6 | ||||
| M | S | M | S | M | S | M | S | |
| Алгоритм 6 | 14 | 900 | 30 | 725 | 62 | 632 | 126 | 529 |
| Алгоритм максимальної пам'яті. | 469 | 58 | 750 | 46 | 1280 | 38 | 2079 | 33 |
Размещено на Allbest.ru
 2020-09-24
2020-09-24 120
120







