Якщо в криптосистемі є резерви пам'яті, їх можна задіяти для подальшого збільшення швидкості обчислень. Ідея в тому, що замість точки  можна експоненціювати і надалі складати суміжні блоки або вікна шириною
можна експоненціювати і надалі складати суміжні блоки або вікна шириною  в
в 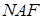 - поданні точки
- поданні точки 
Для цього розраховується за допомогою алгоритму 2 трійкове число 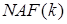 , що потім може розбиватися на блоки довжиною, не менше
, що потім може розбиватися на блоки довжиною, не менше 
Назвемо  - вікном числа
- вікном числа  непарний коефіцієнт
непарний коефіцієнт  утримуючий хоча б один ненульовий елемент. Зазначимо, що
утримуючий хоча б один ненульовий елемент. Зазначимо, що 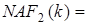
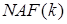 . Наприклад, при
. Наприклад, при 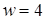 маємо вісім різних значень
маємо вісім різних значень 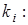
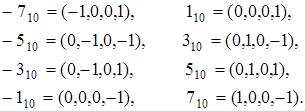
Цих вікон достатньо для формування числа 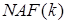 довільної довжини
довільної довжини  . Зазначимо, що парні коефіцієнти в
. Зазначимо, що парні коефіцієнти в 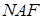 - поданні числа
- поданні числа 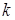 надлишкові, тому що вони утворяться подвоєнням непарних. На першому етапі передрозрахунків розраховуються й записуються на згадку вісім точок:
надлишкові, тому що вони утворяться подвоєнням непарних. На першому етапі передрозрахунків розраховуються й записуються на згадку вісім точок:  і
і 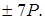
У загальному випадку в пам'яті зберігається 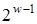 точок. Число
точок. Число  може бути визначене за допомогою модифікованого алгоритму 2. Модифікація полягає в тому, що: на кроці 2.1 замість
може бути визначене за допомогою модифікованого алгоритму 2. Модифікація полягає в тому, що: на кроці 2.1 замість 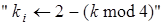 необхідно записати
необхідно записати 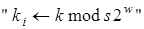 , де
, де  означає ціле число
означає ціле число  , певне в інтервалі
, певне в інтервалі 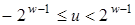 . Далі обчислюється точка
. Далі обчислюється точка 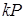 згідно з алгоритмом 4.
згідно з алгоритмом 4.
Алгоритм 4.
Вхід: 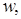
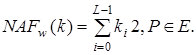
Вихід: 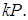
1. 
2. 
3. 
3.1 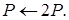
3.2 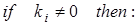
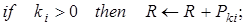
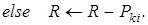
4. 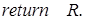 .
.
Нехай, наприклад, 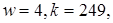 при цьому
при цьому  й
й 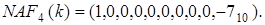 Використання трійкового
Використання трійкового 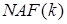 вимагає, мабуть, двох додавань точок, тоді як у другому випадку за рахунок попереднього розрахунку точки
вимагає, мабуть, двох додавань точок, тоді як у другому випадку за рахунок попереднього розрахунку точки 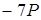 достатньо одного додавання. Число подвоєнь однаково в обох випадках. Зрозуміло також, що виграш за рахунок вікна з'являється лише при порівняно більших довжинах
достатньо одного додавання. Число подвоєнь однаково в обох випадках. Зрозуміло також, що виграш за рахунок вікна з'являється лише при порівняно більших довжинах  числа
числа 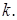
Перший крок алгоритму 4 у загальному випадку вимагає 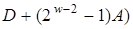 групових операцій із точками кривої. На третьому кроці складність обчислень оцінюється середнім числом
групових операцій із точками кривої. На третьому кроці складність обчислень оцінюється середнім числом 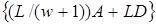 групових операцій додавання й подвоєння. Збільшення ширини
групових операцій додавання й подвоєння. Збільшення ширини 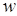 вікна веде до збільшення складності обчислень на першому кроці (і об'єму пам'яті) і зниження тимчасової складності на третьому кроці. Для значень
вікна веде до збільшення складності обчислень на першому кроці (і об'єму пам'яті) і зниження тимчасової складності на третьому кроці. Для значень 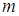 розширення поля порядку 180-260 оптимальним виявляється вікно шириною
розширення поля порядку 180-260 оптимальним виявляється вікно шириною  , а при
, а при 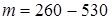 - вікно шириною
- вікно шириною 
Метод Монтгомері
Розглянемо метод Монтгомері. Нехай 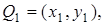
 з
з 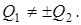 Позначимо
Позначимо 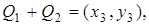
 Можна перевірити, що
Можна перевірити, що
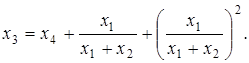 (1)
(1)
Отже, знаючи  - координати точок
- координати точок 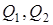 й
й  , можна обчислити
, можна обчислити  координати точок
координати точок 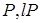 й
й 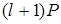 , перейти до пари
, перейти до пари 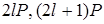 , або до пари
, або до пари  .
.
Кожна така ітерація вимагає одного подвоєння й одного додавання з використанням формули (1).
Після останньої ітерації, 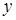 - координата точки
- координата точки 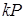 може бути відновлена з
може бути відновлена з  - координати точки
- координати точки 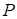 й
й  - координат точок
- координат точок  і
і  за формулою
за формулою
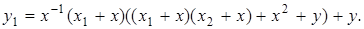
Використовуючи проективні координати, можна позбутися від інвертування, і кожна ітерація вимагатиме шість множень. Усього ж трудомісткість алгоритму 5, що реалізує метод експоненціювання Монтгомері, дорівнює  причому алгоритм не вимагає додаткової пам'яті на зберігання попередньо обчислених змінних, а час його роботи не залежить від значення
причому алгоритм не вимагає додаткової пам'яті на зберігання попередньо обчислених змінних, а час його роботи не залежить від значення 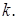
Алгоритм 5. Метод експоненціювання Монтгомері.
Вхід: 
Вихід: 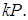
1. 
2. 
2.1 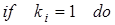
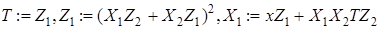
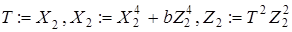

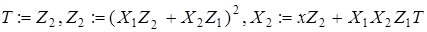
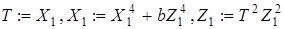
3.1 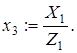
3.2 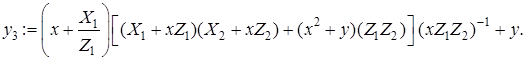
4. 
Алгоритм 5 вимагає однієї інверсії, а не двох, тому що можна обчислити
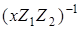 , а
, а  потім отримати множенням на
потім отримати множенням на 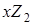 . Можна домогтися істотного збільшення продуктивності, якщо операцію подвоєння замінити операцією ділення точки на два. Виграш до 40% при цьому досягається у зв'язку з відсутністю операції інверсії елемента в полі. Крім того, групові операції послідовних ділень у НБ зводяться практично до однієї операції множення в полі.
. Можна домогтися істотного збільшення продуктивності, якщо операцію подвоєння замінити операцією ділення точки на два. Виграш до 40% при цьому досягається у зв'язку з відсутністю операції інверсії елемента в полі. Крім того, групові операції послідовних ділень у НБ зводяться практично до однієї операції множення в полі.
 2020-09-24
2020-09-24 144
144








