Принцип действия баллистического гальванометра

Баллистический гальванометр является электромеханической системой, поскольку движение его рамки определяется как механическими, так и электромагнитными силами, возникающими при взаимодействии тока в рамке с магнитным полем в кольцевом зазоре. Если гальванометр работает в баллистическом режиме, то процессы в нём можно разделить на два последовательных этапа: 1) в короткое время 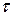 протекания импульса тока через рамку; 2) после окончания импульса тока. Рассмотрим каждый этап в отдельности.

Пусть через рамку в течение короткого времени 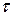 проходит импульс тока  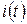(рис. 2). Тогда при  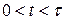сила 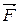, действующая на каждую из двух сторон рамки, находящихся в кольцевом зазоре между магнитом и цилиндром (рис. 3), определяется формулой Ампера

,

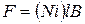(1)

где 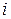 - ток в обмотке рамки,  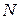- число витков обмотки,  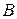- магнитное поле в зазоре,  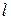- длина части рамки, находящейся в зазоре, т.е. длина вертикальной части рамки на рис. 1.

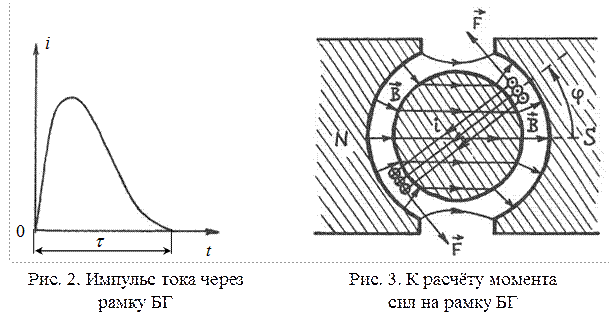
Пара сил 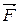 создает вращающий момент на рамку

,

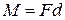(2)

где 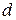 - части рамки, лежащей на торце цилиндрического сердечника. Поле  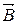в зазоре имеет радикальную структуру, следовательно, силы 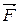, действующие на стороны рамки, перпендикулярны к её плоскости в достаточно широком диапазоне углов поворота рамки. А это значит, что момент этих сил практически не зависит от угла поворота в рабочем диапазоне углов. Формулу (2) с учетом (1) можно записать в виде

,

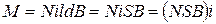(3)

где 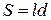 - площадь рамки. Проинтегрируем (3) по времени от 0 до :

,

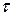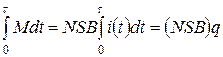где 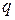 - заряд, прошедший через рамку за время 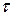. С другой стороны, из уравнения вращения  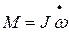имеем:

;

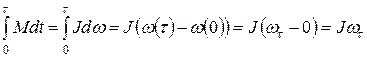здесь 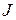 - момент инерции всей подвижной системы БГ, т.е. рамки со стрелкой (зеркальцем) и грузом. Таким образом, сразу после прохождения по обмотке рамки короткого импульса тока, перенесшего заряд 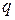, рамка приобрела угловую скорость 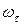, пропорциональную этому заряду:

.

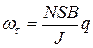(4)

Однако за короткое время 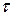 рамка не успевает заметно сместиться от равновесия, так что действие на рамку кратковременной силы Ампера здесь аналогично удару в механике.

На этом первый этап электромеханического процесса в БГ заканчивается. Дальнейший характер движения рамки при начальной скорости (4) будет определяться действующими на неё силами, а точнее – моментами сил. Определим эти моменты.

Во-первых, при отклонении рамки на угол 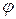 от равновесия (рис. 3) нить подвеса скручивается и создает вращающий момент

,

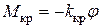(5)

где 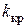 - коэффициент крутильной упругости нити.

Во-вторых, при движении с угловой скоростью 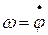 вся подвижная система БГ испытывает вязкое трение о воздух. Момент сил этого трения пропорционален угловой скорости и направлен против вращения:

,

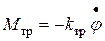(6)

где 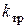 - коэффициент вязкого трения о воздух при вращении.

И, наконец, в третьих, при движении рамка испытывает и электромагнитное торможение, которое может быть весьма существенным и определять характер движения рамки после получения ею стартовой угловой скорости 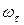 (4). Его природа состоит в следующем.

При вращении рамки с угловой скоростью 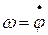 в двух её сторонах, движущихся в магнитном поле зазора 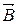, наводится ЭДС индукции

,

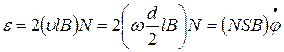следовательно, в цепи рамки будет индуцирован ток

,

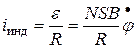где 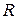 - общее сопротивление цепи рамки БГ. Но на проводник с током в магнитном поле действует сила Ампера, которая препятствует движению проводника, породившему этот ток. В данном случае она препятствует вращению рамки, причем момент этой тормозящей сила Ампера определяется по формуле, аналогичной (3):

.

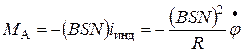(7)

Формула (7) и описывает электромагнитное трение при вращении рамки в магнитном поле. Момент силы этого трения пропорционален угловой скорости рамки и обратно пропорционален полному активному сопротивлению в цепи рамки. При измерениях емкости (разд. 1.4, рис. 6) в цепи БГ установлен конденсатор, разрывающий эту цепь, так что 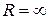. В этом случае электромагнитного трения нет и рамка при вращении испытывает только небольшое вязкое трение о воздух. При измерениях взаимной индуктивности  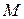двух катушек (разд. 1.5, рис. 7) в цепи БГ находится вторичная катушка  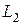и некоторое добавочное сопротивление 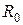, так что полное сопротивление цепи БГ

,

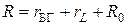где 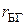 - сопротивление рамки БГ,  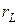- внутреннее активное сопротивление катушки  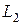(роль 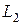, как и 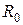, будет показана в разд. 1.5). В этом случае электромагнитное торможение может быть весьма большим.

Таким образом, общее уравнение вращения рамки

,

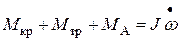где 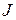 - момент инерции подвижной системы БГ, после подстановки в него (5), (6) и (7) принимает вид:

.

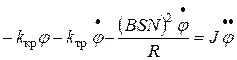Его удобно записывать в стандартной форме уравнения свободных затухающих колебаний:

.

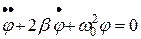(8)

Здесь параметр

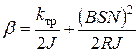(9)

называется коэффициентом затухания, причем первое его слагаемое определяется трением о воздух, а второе – электромагнитным торможением. Параметр 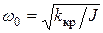 называется собственной частотой колебаний.

Из теории свободных колебаний известно, что если 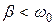, то уравнение (8) описывает колебательный процесс с затуханием, т.е. колебания с экспоненциально убывающей амплитудой. Этот вариант можно наблюдать при измерениях ёмкости, когда цепь БГ разомкнута и  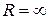(см. разд. 1.4 и рис. 6). В правой части (9) при этом остаётся лишь первое слагаемое (электромагнитного торможения нет), а так как трение рамки БГ о воздух достаточно мало, то 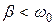. В этом случае решение уравнения (8) имеет вид

.

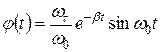(10)

График этого процесса показан на рис. 4.

При измерениях взаимной индуктивности катушек (разд. 1.5) общее сопротивление 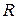 в цепи БГ, как правило, настолько невелико (несколько кОм), что второе слагаемое в (9) оказывается значительно больше первого, величина  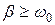и колебательный процесс (10) вследствие большого электромагнитного торможения вырождается в апериодический

,

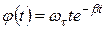(11)

вид которого показан на рис. 5: рамка после первого отброса медленно возвращается к положению равновесия.

Из формул (10) и (11) видно, что максимальный угол отклонения рамки, обозначенный на рис. 4 и 5 через 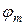, пропорционален начальной скорости 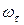, которая в свою очередь, согласно формуле (4), пропорциональна заряду 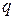, прошедшему через рамку. Этот максимальный угол  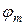называется баллистическим отбросом. Таким образом, баллистический отброс 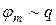*). Эту линейную зависимость можно записать в виде

;

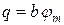(12)

коэффициент пропорциональности  в этой зависимости называется баллистической постоянной гальванометра. Поскольку баллистический отброс 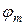 практически выражается в делениях шкалы БГ, то постоянная  имеет размерность [Кл/дел] и показывает, какой заряд 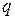 вызывает смещение стрелки на  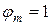деление.

Итак, БГ в баллистическом режиме измеряет заряд, прошедший через рамку при импульсе тока.

Важно отметить, что баллистическая постоянная 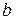 существенно зависит от общего сопротивления  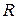в цепи рамки, поэтому все баллистические измерения в некотором цикле опытов проводят при неизменном общем сопротивлении  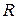в цепи БГ.

Линейная зависимость (12) между 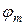 и 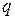 лежит в основе использования БГ для измерений многих электромагнитных величин, связанных определенным образом с зарядом 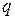. Методы таких измерений основаны на сравнении искомой величины с соответствующей эталонной, т.е. это – методы сравнения. В данной работе БГ используется для измерений ёмкости конденсаторов и взаимной индуктивности катушек.