Графическое представление информации

1. Полигон частот: вдоль горизонтальной оси отмечаем значения оценок, вдоль вертикальной – частоту (или относительную частоту). Наносим соответствующие точки и соединяем линией (см. рис. 1).

Рис. 1. Полигон частот

2. С толбчатая диаграмма. Оси те же, а значения отмечаем прямоугольником соответствующей высоты (см. рис. 2).

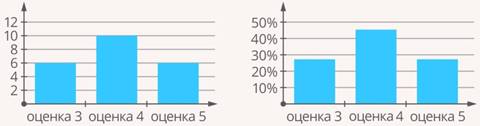
Рис. 2. Столбчатая диаграмма

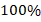3. Для наглядности можно использовать и круговую диаграмму. Для ее построения круг необходимо разбить на секторы, центральные углы которых пропорциональным частотам (и, соответственно, относительным частотам). Углы удобно считать через относительные частоты: полный круг () соответствует , тогда одному проценту соответствует центральный угол 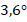(см. рис. 3).

В нашем примере оценкам 3 и 5 соответствует угол 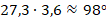, а оценке 4:

Рис. 3. Круговая диаграмма

Итак, мы увидели, что для увеличения наглядности информации, данные можно:

1. упорядочить;

2. записать в таблицу;

3. представить графически.

В рассмотренном примере у нас было всего 3 различных значения оценки. Если же различных значений будет больше, то все эти способы потеряют наглядность.

А в жизни….

Вернемся к примеру с ростом всех детей в школе. Если минимальный рост школьника 142 см, а максимальный – 189 см, то у нас будет целых 48 столбцов в таблице и на диаграмме. Не очень наглядно (см. рис. 4).

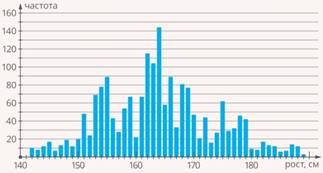
Рис. 4. 48 столбцов на диаграмме

В таком случае данные удобно объединить по интервалам. Например, весь диапазон разбить на интервалы по 10 см: от 140 до 150, от 150 до 160 и т. д. Для каждого интервала будем считать количество школьников, рост которых попадает в данный интервал. Естественно, каждого ученика нужно учесть только в одном интервале, поэтому нужно заранее оговорить, куда включать данные, которые попадают на границы интервалов. Объединив данные по интервалам, получим наглядное представление данных:

Рост, см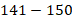
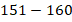
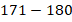
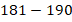
Частота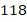

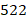
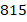
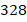
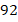
Графическое представление также будет выглядеть более наглядно, чем до объединения в интервалы (см. рис. 5).

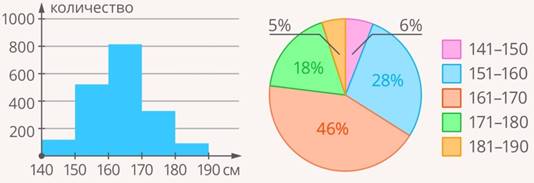
Рис. 5. Гистограмма и круговая диаграмма

Отметим отличия гистограммы от столбчатой диаграммы:

1. Прямоугольники принято рисовать сомкнутыми.

2. Основание прямоугольника соответствует длине интервала, а не выбирается произвольно.

ХАРАКТЕРИСТИКИ

Примере:

Количество ошибок в диктанте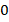
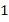
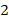
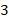
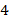
Количество учеников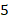

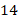
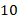
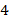
Во-первых, оценим значения, которые может принимать исследуемая величина – количество ошибок в диктанте: максимальное значение – 4, минимальное значение – 0.

В среднем…вот тут нет однозначного ответа. Выделяют несколько характеристик, которые можно назвать «средним значением».

1. Среднее арифметическое – сумма всех численных значений, деленная на их количество. Всего было сделано ошибок: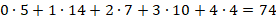

Всего учеников: 40, тогда среднее арифметическое равно:

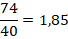
Но среднее арифметическое не всегда будет давать правильное представление о выборке. Например, если 9 человек написали диктант без ошибок, а 1 человек сделал в нем 20 ошибок, то среднее арифметическое количества ошибок будет равно:

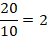
Т. е. может показаться, что эта группа написала диктант хуже, чем первая, хотя, фактически, ее «утянул на дно» один человек. В таком случае можно использовать другие характеристики, которые уменьшают влияние таких крайних значений, например медиану ряда.

2. Медиана – значение среднего элемента в упорядоченном ряду данных. Учеников 40, значит, в упорядоченном ряду данных о количестве ошибок будет 40 элементов:

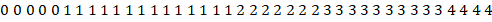
Средними элементами будут 20-й и 21-ый. Посмотрим, что это за элементы: первые 5 чисел – нули, затем – 14 единиц. Т. е. 19-й элемент – еще единица, далее идут 7 двоек. Значит, 20-й и 21-ый элементы – это двойки:

Медиана равна 2. Если же средние элементы различны, то медианой обычно считают их полусумму. У нечетного количества данных медианой будет просто центральный элемент упорядоченного ряда (например, медиана ряда 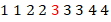равна 3).

Другим минусом среднего арифметического как величины, которая характеризует выборку, является то, что ее не всегда можно использовать. Действительно, если среднее значение размера обуви у клиентов фабрики 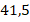, это не значит, что фабрика должна выпускать обувь такого размера – в таком случае она попадет в «дырку от бублика» (центр тяжести бублика находится в его центре – но использовать это, чтобы подвесить его или каким-то другим способом обеспечить положение равновесия, не получится). Поэтому для обувной фабрики более полезной будет информация о наиболее часто встречающихся размерах обуви – самых популярных.

3. Для этого можно использовать моду – величину, имеющую наибольшую частоту (отсюда и название). В нашем примере мода равна 1 (частота 14 наибольшая):

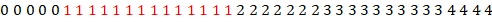
Мода обычно равна или близка средним значениям. Если сразу несколько значений ряда встречаются одинаково наиболее часто, то обычно говорят, что моды у ряда нет.

Мы выделили 3 характеристики, которые можно назвать «средними значениями». Но чаще всего под «средним значением» понимают именно среднее арифметическое.

Для оценки разброса есть несколько основных характеристик:

1. Размах – разность между максимальным и минимальным значениями.

2. Дисперсия – это среднее арифметическое квадратов отклонений данной величины от ее среднего значения:

где 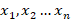– значения исследуемой величины:

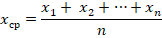
Дисперсия показывает, насколько сильно данные отклоняются от их среднего значения. Чем больше дисперсия, тем больше разброс данных. Для вычисления дисперсии данную формулу удобно преобразовать к виду:

где: