2020-09-26
184
| Признаки | Варианты моделей | Их модификации | |
| Для систем снабжения | По структуре | Эшелонированные | |
| однокаскадные | - | ||
| По динамикевыполнения операций снабжения | Статические (одноразовые заказы на создание запаса) | - | |
| Динамические(многоразовые заказы на создание запаса) | - | ||
| По числу компонентов | однономенклатурные | - | |
| многономенклатурные | - | ||
| В зависимости от спроса |
По стационарности
| Стационарные | - |
| Нестационарные | -периодические - непериодические (зависимый и независимый от спроса в предыдущем периоде) | ||
| По полноте имеющейся информации | Детерминированные (без учета факторов случайности) | - | |
| Стохастические (вероятностные) | -с известным распределением спроса - с неизвестным распределением спроса | ||
| По дискретности | Непрерывные | - | |
| Дискретные (прерывные, с целочисленными случайными величинами) с объемом требований | - постоянным -переменным -случайным | ||
| По связис различными компонентами | Модель со связью (зависимый спрос) | - | |
| Связь отсутствует (независимый спрос) | - | ||
| Пополнение запасов | По задержкам | Модели с отсутствием задержек | - |
| Модели с фиксированными задержками | - целое число периодов - дробное число периодов | ||
| Модели с случайными задержками | - | ||
| По способу ликвидации срывов поставок | Модель с накопление отказов до очередной поставки (с планируемым дефицитом) | - | |
| Экстренные модели поставок | - | ||
| По объему поставки | Модель поставки равная заказу | - | |
| Случайная величина | - | ||
|
| |||
|
| |||
|
| |||
|
| |||
|
| |||
| Стратегия (Простейшая) |
Тип
| Периодическая (заказ производиться в каждом периоде t) | |
| Критических уровней (при снижении текущего запаса до порогового значение)
| |||
T h0OoGJVYnykJdQhdxrkvazTKz12HlrKz640KNPYV170aqdy0fBFFS25UY+lCrTrc1VheDlcj4X1U 4zaJX4f95by7/RzFx/c+Rimfn6btGljAKfzD8KdP6lCQ08ldrfaslTATL4JQCpI0AUbEKhG0OUlY LkQKvMj5/Q/FLwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAA AAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAA AAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQCsUDg4kwsAALpwAAAOAAAA AAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQBi8gxc4gAAAAsBAAAP AAAAAAAAAAAAAAAAAO0NAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA/A4AAAAA ">
| Заказы (2) |
| Поставщик (4) (производитель) (4) |
| Складская (3) система Уровень запаса (3) |
| Спрос (1) Потребитель Потребитель |
| Стратегия (5) управления запасами |
| Правило (6) выполнения заказа |
| МР (ГП) |
| МР (ГП) |
| расход |
| пополнение |
| Материальный поток |
| Информационный поток |
Изучение теории управления запасами следует рассматривать с общей модели, в основе которой находится модель управления запасами без дефицита, которую вы изучили по дисциплине ОЛУЦП. Эта модель показана на рис. 4.2, 4.3.
Рис. 4.2. Общая модель управления запасами
| Q |
| Qmax |
|
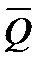
| QT |
| Qстр СТР |
| 0 |
| t |
| τв з |
| τc з |
| τв з |
| tз |
| t п |
| tз |
| t п |
| t п |
| tз |
| D=const |
| страховой запас |
| qз |
| qп |
| qп |
| qп |
| qз |
| qз |
| τcп |
Рис.4.3. Параметры и механизм функционирования модели управления запасами без дефицита
Простейшая модель управления запасами без дефицита, которую еще называют классической, основана на формуле экономического размера заказа (EOQ-EconomicOrderQuantity) Уилсона (Вилсона) полученной в 1913 г. В этой модели оптимальные размеры заказа и запаса совпадают (рис 4.3).
Для получения формулы Уилсона введем условные обозначения: Q – объем запаса; T - период хранения запасов; D – спрос; qз – размер заказа; q* - оптимальный размер запаса и заказа; q1 – точка заказа; tg – время доставки; n – число заказов за период Т; С1 – стоимость доставки одного заказа; С2 – стоимость хранения единицы продукции в единицу времени;
СD – стоимость доставки заказов за период Т; СX – стоимость хранения запасов за период Т; С – стоимость ЛС за период Т.
Последовательность вывода формулы Уилсона следующая /4/. Пусть стоимость закупки не зависит от размера заказа. Тогда стоимость ЛС:
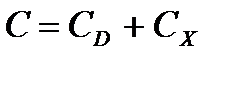(4.1)
Стоимость доставки. Потребность в продукции составляет D, каждый заказ имеет размер q, тогда количество заказов за время 
, а стоимость доставки 
.
Стоимость хранения запаса. Для этого рассматривают среднее количество продукции, составляющей запас в течение одного цикла. Размер запаса меняется от Q до q, поэтому средний уровень запаса q/2. С учетом С2, стоимость хранения единицы продукции за время Т равно С2Т отсюда СX всей продукции за время Т:
(4.2)
Суммарная стоимость: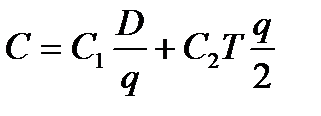 
(4.3)
Нужно определить такой размер запаса и заказа, при котором стоимость будет минимальна: С является функцией от q, следовательно для определения Сmin нужно взять производную С по q и приравнять их к нулю:
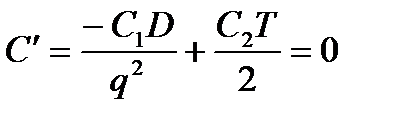(4.4)
Отсюда:
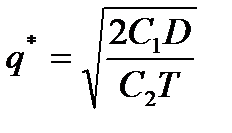(4.5)
- формула Уилсона, где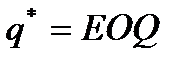 
- экономичный размер заказа.
Подставив в выражение для CD и СX - q* получим оптимальные значения CD и СX.
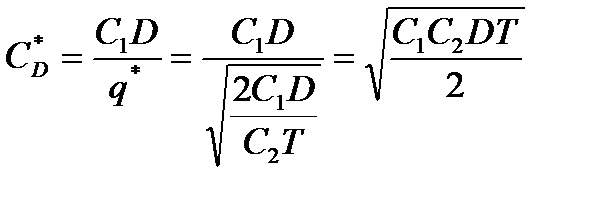
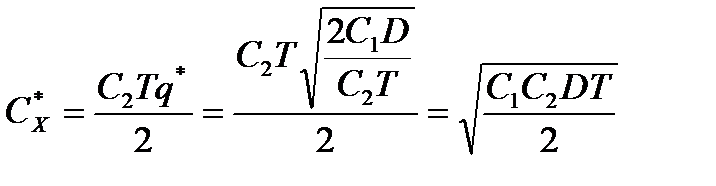(4.6)
| С |
| q |
| q*= EOQ |
|
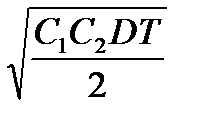
| Общая стоимость |
| Стоимость хранения |
| Стоимость доставки |
Составляющие общих затрат, по разному зависят от размера заказа рис. 4.4.
Рис. 4.4. Изменение стоимости хранения и доставки от размера поставки
При небольшом размере заказа определяющей величиной является стоимость доставки. Это означает, что заказы доставляются часто и небольшой величины. При увеличении размера заказа определяющей величиной становиться хранение запаса. Такие заказы поставляются редко и значительно увеличивают размер хранящейся на складе продукции.
Из графика также видно, что небольшие изменения размера заказа в окрестностях точки EOQ не ведут к существенному изменению стоимости. Следовательно, кроме EOQ можно выбрать еще несколько размеров заказа, которые не приведут к существенному увеличению стоимости данной ЛС. Это свойство стоимости позволяет учесть, например, производство поставщиком продукции партиями определенного размера или транспортировки заказа в размере, несколько отличающимся от рассчитанного выше.
