Рассмотрим примеры на исследование сходимости несобственных интегралов.
Пример 1.
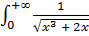
 - несобственный интеграл от положительной функции одновременно
- несобственный интеграл от положительной функции одновременно 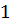 и
и  рода, так как промежуток интегрирования - бесконечный, а подынтегральная функция - неограниченная (
рода, так как промежуток интегрирования - бесконечный, а подынтегральная функция - неограниченная (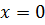 - особая точка).
- особая точка).
Разобьем промежуток интегрирования на два промежутка и исследуем каждый из полученных несобственных интегралов:
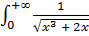
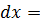
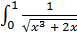
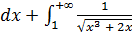
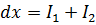 .
.
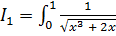
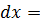
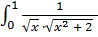
 ,
, 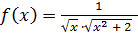
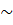
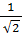 ∙
∙ 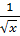
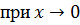 ;
;
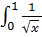
 - это сходящийся «эталонный» интеграл 2 рода (
- это сходящийся «эталонный» интеграл 2 рода (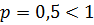 ) ⇒
) ⇒ 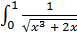
 - сходится (по второму признаку сравнения).
- сходится (по второму признаку сравнения).
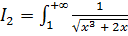
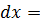
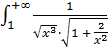
 ,
, 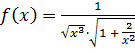
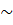
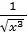
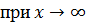 ;
;
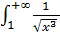
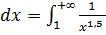
 - это сходящийся «эталонный» интеграл 1 рода (
- это сходящийся «эталонный» интеграл 1 рода (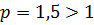 ) ⇒
) ⇒ 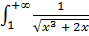
 - также сходится (по второму признаку сравнения).
- также сходится (по второму признаку сравнения). 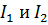 - сходятся⇒
- сходятся⇒ 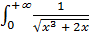
 - сходится.
- сходится.
Пример 2.
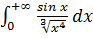 - несобственный интеграл одновременно
- несобственный интеграл одновременно 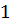 и
и  рода, так как промежуток интегрирования - бесконечный, а подынтегральная функция - неограниченная (
рода, так как промежуток интегрирования - бесконечный, а подынтегральная функция - неограниченная (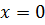 - особая точка).
- особая точка).
Разобьем промежуток интегрирования на два промежутка и исследуем каждый из полученных несобственных интегралов:
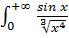
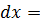
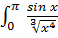
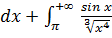
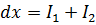 .
.
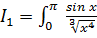
 - несобственный интеграл
- несобственный интеграл  рода от положительной функции,
рода от положительной функции, 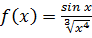
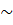
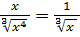
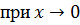 ;
; 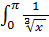
 – это сходящийся «эталонный» интеграл 2 рода (
– это сходящийся «эталонный» интеграл 2 рода (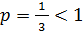 ), по второму признаку сравнения несобственный интеграл
), по второму признаку сравнения несобственный интеграл 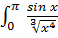
 - сходится.
- сходится.
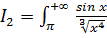
 - несобственный интеграл 1 рода от знакопеременной функции - сходится абсолютно, так как
- несобственный интеграл 1 рода от знакопеременной функции - сходится абсолютно, так как 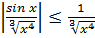 и
и 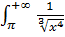
 - это сходящийся «эталонный» интеграл 1 рода (
- это сходящийся «эталонный» интеграл 1 рода (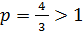 ).
).
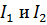 - сходятся ⇒
- сходятся ⇒ 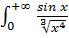
 - сходится.
- сходится.
Пример 3.
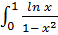
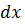 - несобственный интеграл
- несобственный интеграл  рода от отрицательной функции с двумя особыми точками:
рода от отрицательной функции с двумя особыми точками: 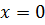 и
и 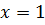 . Разобьем промежуток интегрирования на два промежутка и исследуем каждый из полученных несобственных интегралов:
. Разобьем промежуток интегрирования на два промежутка и исследуем каждый из полученных несобственных интегралов:
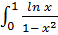
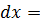
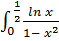
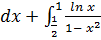
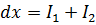 .
.
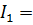
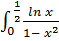
 ,
, 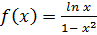
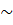
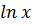
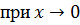 ;
; 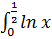
 - сходится
- сходится
(см. § 6) ⇒ 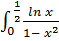
 - сходится (по второму признаку сравнения).
- сходится (по второму признаку сравнения).
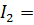
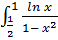
 ,
, 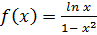 ;
; 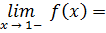
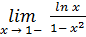
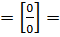
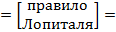
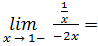
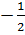 ⇒
⇒ 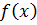 - ограниченная функция на промежутке
- ограниченная функция на промежутке 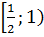 ⇒
⇒ 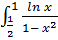
 – это собственный интеграл, значит, он сходится;
– это собственный интеграл, значит, он сходится; 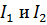 - сходятся ⇒
- сходятся ⇒ 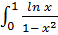
 - сходится.
- сходится.
Пример 4.
Исследуем на сходимость несобственный интеграл 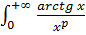
 , т.е. найдем все значения параметра
, т.е. найдем все значения параметра 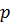 , при которых данный несобственный интеграл сходится.
, при которых данный несобственный интеграл сходится.
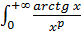
 - несобственный интеграл от положительной функции одновременно
- несобственный интеграл от положительной функции одновременно 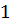 и
и  рода, так как промежуток интегрирования - бесконечный, а подынтегральная функция – неограниченная (есть особая точка:
рода, так как промежуток интегрирования - бесконечный, а подынтегральная функция – неограниченная (есть особая точка: 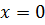 ).
).
Разобьем промежуток интегрирования на два промежутка и исследуем каждый из полученных несобственных интегралов:
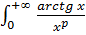
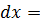
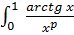
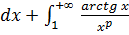
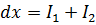 .
.
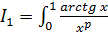
 ,
, 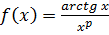
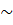
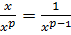
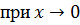 ;
; 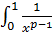
 - это «эталонный» интеграл 2 рода - сходится при
- это «эталонный» интеграл 2 рода - сходится при 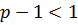 , т. е. при
, т. е. при  , и расходится при
, и расходится при 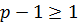 , т. е. при
, т. е. при 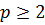 .
.
Следовательно, 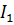 - также сходится при
- также сходится при  и расходится при
и расходится при 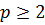 .
.
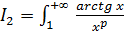
 ,
, 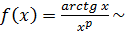
 ∙
∙ 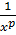
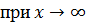 ;
; 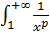
 - это «эталонный» интеграл 1 рода - сходится при
- это «эталонный» интеграл 1 рода - сходится при 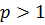 и расходится при
и расходится при 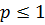 . Следовательно,
. Следовательно, 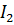 - также сходится при
- также сходится при 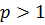 и расходится при
и расходится при 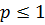 .
.
Итак, 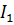 - сходится при
- сходится при  , а
, а 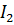 - сходится при
- сходится при 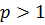 . Значит,
. Значит,
несобственный интеграл 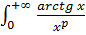
 сходится при
сходится при 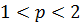 .
.
Пример 5.
Исследуем на сходимость несобственный интеграл
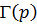
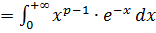 .
.
Представим 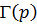 в виде суммы двух интегралов:
в виде суммы двух интегралов: 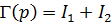 ,
,
где 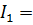
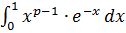 ,
, 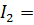
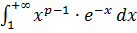 .
.
Если 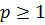 , то
, то 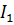 - собственный интеграл; если
- собственный интеграл; если  , то
, то 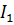 - несобственный интеграл
- несобственный интеграл  рода с единственной особой точкой
рода с единственной особой точкой 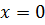 ;
;
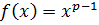 ∙
∙ 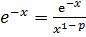
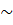
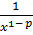
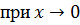 ;
; 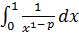 - сходится при
- сходится при 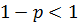 , т.е. при
, т.е. при 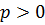 , и расходится при
, и расходится при 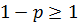 , т.е. при
, т.е. при 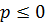 .
.
Следовательно, 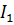 также сходится при
также сходится при 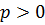 , и расходится при
, и расходится при 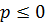 .
.
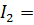
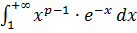 - несобственный интеграл
- несобственный интеграл 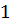 рода; покажем, что этот интеграл сходится при
рода; покажем, что этот интеграл сходится при 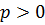 .
.
Известно, что 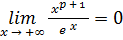 "
" 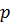 ; значит, существует число
; значит, существует число 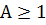 такое, что
такое, что 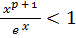 "
" 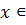
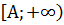 ;
; 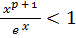 ⇔
⇔ 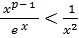 ;
; 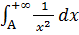 – сходится («эталонный» интеграл 1 рода); значит, по первому признаку сравнения
– сходится («эталонный» интеграл 1 рода); значит, по первому признаку сравнения 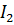 - также сходится "
- также сходится " 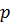 .
.
Следовательно, 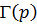 - сходится при
- сходится при 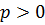 .
.
Замечание. Рассмотренный интеграл 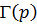 является функцией параметра
является функцией параметра 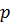 . Эта функция называется гамма - функцией. Гамма - функция имеет широкое применение в теории вероятностей, математической статистике и в самом математическом анализе.
. Эта функция называется гамма - функцией. Гамма - функция имеет широкое применение в теории вероятностей, математической статистике и в самом математическом анализе.
Пример 6. Исследуем на сходимость несобственный интеграл
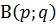
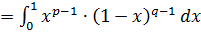 .
.
При  особой точкой будет
особой точкой будет 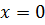 , а при
, а при 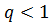 особой точкой будет
особой точкой будет 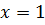 . Пусть
. Пусть 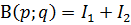 , где
, где
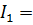
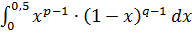 ,
, 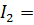
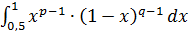 .
.
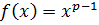 ∙
∙ 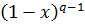
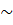
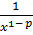
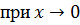 (если
(если 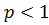 );
);
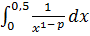 - сходится при
- сходится при 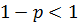 , т.е. при
, т.е. при 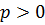 , и расходится при
, и расходится при 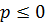 .
.
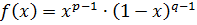
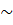
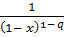
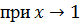 (если
(если 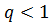 );
);
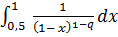 - сходится при
- сходится при 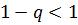 , т.е. при
, т.е. при 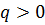 , и расходится при
, и расходится при 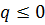 .
.
Итак, 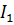 и
и 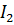 - сходятся при
- сходятся при 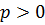 и
и 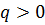 .
.
Следовательно, 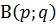 - также сходится при
- также сходится при 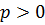 и
и 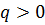 .
.
Замечание. Рассмотренный интеграл 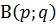 является функцией параметров
является функцией параметров 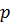 и
и 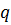 . Эта функция называется бета - функцией. Можно показать, что б ета - функция связана с гамма - функцией следующей формулой:
. Эта функция называется бета - функцией. Можно показать, что б ета - функция связана с гамма - функцией следующей формулой:
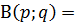
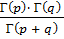 .
.
Контрольные вопросы.
1. Привести примеры несобственных интегралов 1 рода от знакопеременных функций.
2. Дать определение абсолютной сходимости несобственных интегралов 1 рода.
3. Дать определение условной сходимости несобственных интегралов 1 рода.
4. Сходится ли несобственный интеграл 1 рода, если известно, что он:
а) абсолютно сходится; б) условно сходится?
5. Сформулировать признаки сходимости Абеля и Дирихле для несобственных интегралов 1 рода.
6. Привести примеры условно сходящихся несобственных интегралов 1 рода.
7. Дать определение сходимости несобственных интегралов 2 рода, если известно, что единственной особой точкой является: а) правый конец промежутка; б) левый конец промежутка; в) внутренняя точка промежутка.
8. Какие несобственные интегралы 2 рода называются «эталонными»? Указать условия сходимости «эталонных» несобственных интегралов 2 рода.
9. Среди несобственных интегралов 2 рода указать все сходящиеся интегралы:
(а) 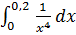 ; (б)
; (б) 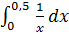 ; (в)
; (в) 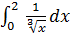 ; (г)
; (г) 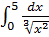 .
.
10. Привести примеры условно сходящихся несобственных интегралов 2 рода.
 2020-10-10
2020-10-10 607
607







