Формы представления логических функций

Логические функцимогут быть представлены различными способами:

1. Словесным описанием (назначением, определением).

2. Таблицей истинности.

3. Аналитическим выражением.

4. Картой Карно.

5. Переключательной схемой.

6. Диаграммой Венна.

7. Геометрическим способом (гиперкубами).

8. Диаграммой двоичного решения.

Если логическая функция зависит от п переменных, то она может быть определена на N=2 ^п наборах логических переменных. Когда функция определена на всех этих наборах, она называется полностью определенной, число различных, полностью определенных логических функций, равно

F = 2^N=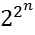

Если на некоторых наборах логическая функция не определена, то она называется не полно­стью определенной. В последнем случае возможны две ситуации: либо нас не интерисует значение функции на некоторых наборах, либо на цифровое устройство нико­гда не поступят некоторые наборы. Имеется три возможности задать не полностью определенную логическую функцию на любом из N наборах: выбрать её значение равным 0, 1 или безразличным значением.

Остановимся подробней на первых трёх формах представления для полностью оп­ределенной логической функции 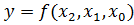, зависящей от 3-х переменных.

Сформулируем её словесное следующим образом: функция принимает истинное значение, когда  истинна либо переменная х₂, либо вместе истинны переменные х₁ и х₀.

Аналитическое выражение для такой функции будет иметь вид

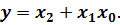
Таблица истинности имеет следующую структуру: в столбце "номер набора" указаны десятичные эквиваленты двоичных 3-х разрядных чисел условно составленных из значений трех аргументов х₂; х₁ и х₀ с учетом соот­ветственно их двоичного веса 4, 2 и 1, то есть наборы расположены в лексикографи­ческой упорядоченности.

Номер набора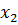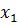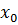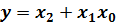
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

 

А

Аналитический способ задания логической функции основывается на использовании элементарных логических операций И, ИЛИ, НЕ. Существуют две формы аналитического представления логической функции.

1. В совершенной дизъюнктивной нормальной форме (СДНФ).

2. В совершенной конъюнктивной нормальной форме (СКНФ).

1. Для того, чтобы получить аналитическое выражение для логической функции в форме СДНФ, нужно записать логическую сумму конституент единицы для тех наборов входных переменных, на которых логическая функция принимает значение,  равное 1, причем, переменная берется без знака инверсии, если ее значение в наборе равно 1 и с инверсией, если ее значение в наборе равно 0. Пользуясь этим правилом получим:

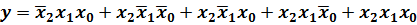
Номер набора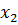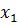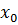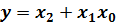
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Нормальной эта форма называется потому, что все члены выражения имеют вид элементарных произведе­ний.

  Дизъюнктивной эта форма называется потому, что все они соединены знаком дизъюнкции (логического сложения).

Совершенной потому, что все члены формулы имеют высший ранг r= п, то есть являются конституентами единицы.

Чтобы сделать логическую функцию более компактной, то есть, чтобы её минимизировать применим рассмотренные нами ранее правила склеивания и тавтологии:

=

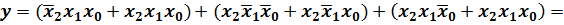
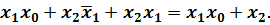
2. Для того, чтобы получить аналитическое выражение для логической функции в форме СКНФ, нужно записать логическую сумму конституент нуля для тех наборов входных переменных, на которых логическая функция принимает значение,  равное 0, причем, переменная берется со знаком инверсии, если ее значение в наборе равно 1 и без инверсии, если ее значение в наборе равно 0. Пользуясь этим правилом получим:

(

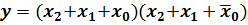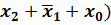
Номер набора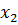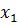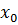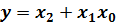
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Нормальной эта форма называется потому, что члены выражения имеют вид элементар­ных сумм.

Конъюнктивной эта форма называется потому, что все члены формулы соединены знаком конъюнкции (логического умножения).

  Совершенной - потому, что все члены формулы имеют высший ранг r= п, являясь конституентами нуля.

Минимизируем её:

( = (                                                           =

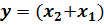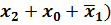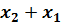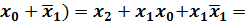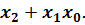
Заметим, что любой логической функции соответствует своя единственная таблица истинности, а, следовательно, для любой логической функции существуют единственные СДНФ и СКНФ. Так как в СДНФ и в СКНФ можно представить любую логическую функцию, а при их построении используются всего три логические опе­рации И, ИЛИ и НЕ, то говорят, что набор этих операций образует функционально полную систему (ФПС), позволяющую реализовать произвольные логические функции.

Совокуп­ность  операций И, ИЛИ и НЕ называют основной функционально полной системой (ОФПС).

Если к полученной выше в форме СДНФ логической функции применить закон двойного отрицания и правило де-Моргана, то получим следующее выражение для той же самой логической функции:

 

                                                      

 

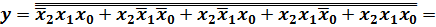
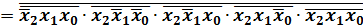
из которого видно, что для представления любой логической функции достаточно только две операции И и НЕ, которые тоже являются ФПС.

 

Если к полученной выше в форме СКНФ логической функции применить закон двойного отрицания и правило де-Моргана, то получим следующее выражение для той же самой логической функции:

=

= .

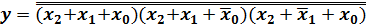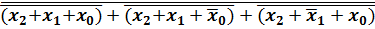из которого видно, что для представления любой логической функции достаточно только две операции И и ИЛИ, которые тоже являются ФПС.

        

    Таким образом, системы функций

    1. И, ИЛИ, НЕ

    2. И, НЕ

    3. ИЛИ, НЕ

 

являются функционально полными, причем первая система сократима, то    есть может быть минимизирована.

    Минимальная функционально полная система функций, удаление из     которой любой функции делает систему неполной, называется базисом. В     современной цифровой схемотехнике широко используются базисы И-НЕ и ИЛИ-НЕ.