Пример. 

Привила развертывания
Эти правила определяют действия обратные склеиванию.
1. Правило развертывания элементарного произведения в логическую сумму элементарных произведений большего ранга (в пределе до r = п, т.е. до конституент единицы, как и будет рассмотрено ниже) следует из законов универсального множества, распределительного закона первого рода производится в три этапа:
- в развертываемое элементарное произведение ранга r вводится в качестве сомножителей n- r единиц, где п - ранг конституенты единицы;
- каждая единица заменяется логической суммой некоторой, не имеющейся в исходном элементарном произведении переменной и ее отрицания: 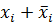 = 1;
= 1;
- производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходного элементарного
произведения ранга г в логическую сумму 2n- r конституент единицы.
Пример: развернуть элементарное произведение 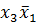 в логическую сумму
в логическую сумму
конституент единицы, зависящих от 4-х переменных. (Последнее следует из того, что максимальный индекс у переменной равен 3).
Решение: отсутствуют переменные 
Пусть п = 3.
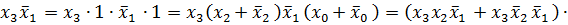
 =
= 
Смысл термина "конституента единицы" можно пояснить следующим примером.
Пусть п = 3.
1=1 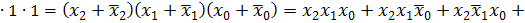
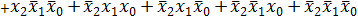
Правило развертывания элементарного произведения используется для минимизации логических функций.
Пример. Пусть требуется минимизировать логическую функцию вида

Видно, что все элементарные произведения имеют одинаковый ранг r = 2, следовательно, правило поглощения нельзя применить; кроме того ни одна пара произведений не является соседней, так как произведения имеют различные переменные, т.е. нельзя применить и правило склеивания. Если же развернуть произведение  до конституент единицы (в данном случае п = 3), то выражение упростится:
до конституент единицы (в данном случае п = 3), то выражение упростится:
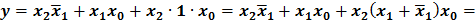
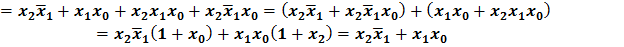
то есть произведение  оказалось лишним.
оказалось лишним.
1. Правило развертывания элементарной суммы ранга r до произведения элементарных сумм ранга п (конституент нуля) следует их законов нулевого множества и распределительного закона второго рода и производится в три этапа:
- в развертываемую сумму ранга r в качестве слагаемых вводится n - r нулей;
- каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной сумме переменной и ее отрицания: 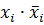 = 0;
= 0;
-получившееся выражение преобразуется на основе распределительного закона второго рода так, чтобы исходная сумма ранга r развернулась в
логическое произведение 2 n - r конституент нуля.
Пример: развернуть элементарную сумму  в логическое произведение
в логическое произведение
конституент нуля, зависящих от 4-х переменных. Последнее следует из того, что максимальный индекс равен 3.
Решение: отсутствуют переменные  .
.
Пусть п = 2.
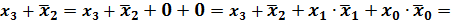


Смысл термина "конституента нуля" можно пояснить следующим примером.
Пусть п = 2.
0=0+0= 
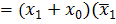 +
+ 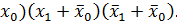
Правило развертывания элементарной суммы также используется для минимизации ФАЛ.
Пример: пусть  Требуется минимизировать данную функцию.
Требуется минимизировать данную функцию.
Операции склеивания и поглощения здесь применить нельзя. Однако, если развернуть сумму 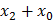 до конституент нуля (в данном случае п = 3), то выражение упростится:
до конституент нуля (в данном случае п = 3), то выражение упростится:
 =
= 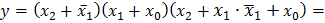
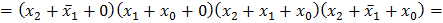

т.е. сумма  оказалась лишней.
оказалась лишней.
Правила склеивания, поглощения и развертывания лежат в основе построения различных методов минимизации логических функций.
 2020-10-10
2020-10-10 439
439








