2020-10-10
538
В основе уравнения равновесия напряжений и совместности деформаций лежит закон сохранения энергии:
. (12.88)
Здесь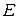 
– потенциальная энергия упругой деформации, 
– внутренняя энергия, изменяющаяся при нагреве от пластической деформации,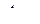 
– работа внешних сил
,
где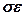 
– плотность энергии (ее количество в единице объема тела). Тогда для всего тела объемом 
. (12.89)
Работа объемных сил 
(магнитных, гравитационных нагрузок, распределенных по объему тела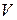 
):
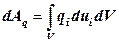, (12.90)
где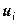 
– перемещения точек тела; работа поверхностных сил 
(контактных нагрузок, распределенных по поверхности тела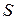 
):
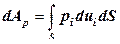. (12.91)
С учетом этих формул выражение закона сохранения энергии приобретает вид:
(12.92)
и обеспечивает такое поведение тела, при котором оно имеет минимум потенциальной энергии и выделяет минимальное количество тепла. Это соответствует равновесию напряжений и совместности деформаций в каждой точке тела. Приращения напряжений 
по каждой оси связаны между собой и с приращением объемной силы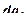 
уравнениями, обеспечивающими равновесие сил, действующих на элементарный объем по каждой оси. Например, для оси (рис. 12.27):
;
.
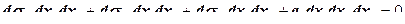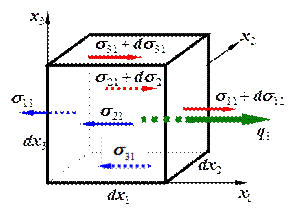
Рис. 12.27. Схема равновесия напряжения по оси x 1
Уравнения совместности деформаций обеспечивают сплошность тела, отсутствие разрывов между смежными объемами материала и их взаимопроникновения. В каждой точке тела существуют три компоненты перемещения 
, которые могут изменяться как угодно, и шесть различных компонент деформации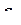 
, причем, согласно формуле (32), каждую компоненту 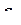можно выразить через компоненты . Следовательно, три из компонент 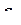связаны уравнениями совместности с остальными тремя.
Если решить интегральное уравнение (12.92), мы получим НДС, в котором напряжения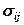 
являются равновесными (находятся в каждой точке в равновесии с объемными силами и поверхностными силами ), а деформации 
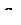- кинематически возможными (не нарушают условий совместности и могут быть найдены по перемещениям ).
Если обеспечить совместность деформаций и задать физические уравнения, связывающие напряжения с деформациями, то из формулы (12.92) можно вывести уравнения равновесия напряжений. Решение этих уравнений обеспечивает получение реального распределения НДС в теле с соблюдением равновесия, совместности и законов упругости и пластичности.
