2020-10-10
260
Основанием для уменьшения размерности модели является наличие информации о компонентах НДС вдоль какой-либо из осей.
Длинное тело. Если вдоль оси 
все поперечные сечения и граничные условия одинаковые, то достаточно рассмотреть один слой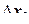 
. Толщину слоя можно выбрать любую, например 
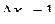. При решении перемещения по осям 
являются неизвестными, а перемещения по оси определяют отдельно следующим образом.
1) Применяют гипотезу плоских сечений:
.
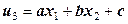Для любой точки 
зависит от координат .
2) Определяют параметры 
. Если граничные условия заданы в перемещениях на торцах трубы, то непосредственно вводят в качестве граничных условий: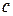 
– общее изменение длины слоя (перемещение точки с координатами 
), 
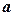– поворот (изгиб) вокруг оси 
, 
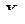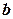– поворот (изгиб) вокруг оси 
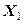. Если условия заданы в силах и изгибающих моментах (
, 
, 
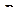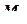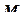), то к списку неизвестных перемещений узлов по осям 1 и 2 добавляют еще три неизвестных и три уравнения:
; (12.109)
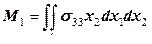; (12.110)
. (12.111)
Наиболее распространенный случай: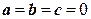 
(плоская деформация). Компоненты деформаций 
определяют из решения по перемещениям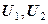 
. Компоненты 
равны нулю, так как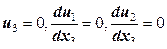 
.
Осевая симметрия. Из условий симметрии следует, что в каждой точке перемещения возможны только по радиусу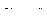 
и вдоль оси симметрии 
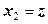, причем они не зависят от угловой координаты точки 
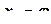. Перемещения в направлении угловой координаты равны нулю, поскольку они нарушают симметрию.
Можно рассмотреть любой сектор модели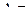 
, например 
рад, или 
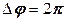рад, или 
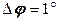. Перемещения по радиусу 
вызывают две компоненты деформации:
1) 
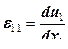: если точки на концах отрезка, направленного по радиусу, имеют разные перемещения, то длина отрезка меняется.
2) 
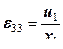: если точка перемещается по радиусу, то меняется длина окружности, проходящей через эту точку.
Таким образом, компоненты деформации 
определяют по перемещениям узлов 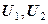, а 
.
Важный момент: при вычислении объема элемента надо учитывать, что толщина элемента в каждой точке разная и зависит от радиальной координаты 
.
