Последовательности и ряды

 

Числовые ряды

Пусть дана функция 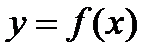. Если областью определения функции является множество натуральных чисел 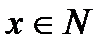, то мы говорим, что значения функции образуют бесконечную числовую последовательность

 

.

 

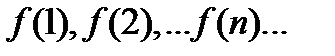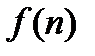называется общим членом последовательности. Для сокращения записи вводится обозначение 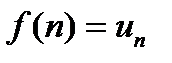. Тогда последовательность можно записать так

 

u ₁, u ₂, u ₃ ,..., u_n …                                                                                            (7.1)

 

Замечание. Областью определения функция 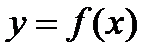может быть и множество натуральных чисел с добавлением нуля .

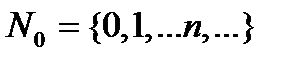Пусть задана бесконечная числовая последовательность чисел (7.1). Числовым рядом  называется последовательность чисел, члены которой соединены знаком плюс, т.е. выражение

  u ₁ + u ₂ + u ₃ +... + u_n  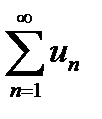+... = .                                                                 (7.2)

числа u ₁, u ₂, u ₃,..., u _n,... называются членами ряда, а u _n общим членом ряда.

Например, числовой ряд

                           

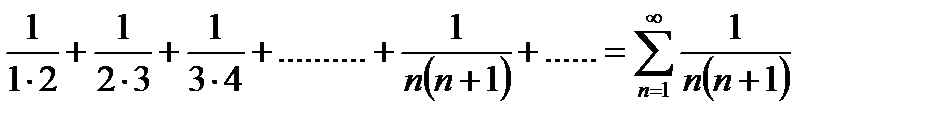
имеет общий член u_n =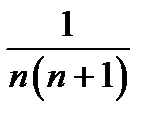

Сходимость и сумма ряда. Частичной суммой S_n называется сумма первых n членов ряда, т.е.

 

 

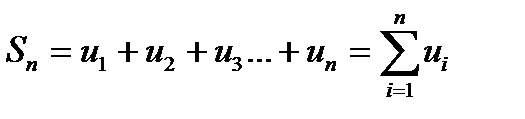
Частичные суммы ряда образуют новую последовательность - последовательность частичных сумм S ₁, S ₂, S ₃,..., S _n,.... Если существует конечный предел последовательности частичных сумм 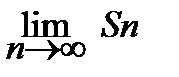= S < ¥, то ряд (7.2) называется сходящимся, а число S - суммой ряда. В этом случае пишут 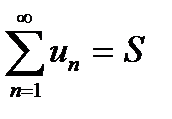. Если такой предел не существует или равен бесконечности, то ряд называют расходящимся.

Разность между рядом и его частичной суммой называется остатком ряда и обозначается .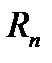

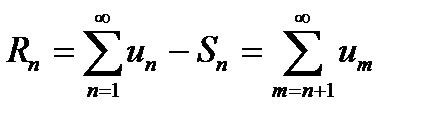или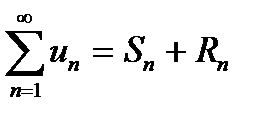

Если предел последовательности частичных сумм бесконечен или не существует, то ряд (7.2) называется расходящимся.

Пример 1. Определить сходимость ряда

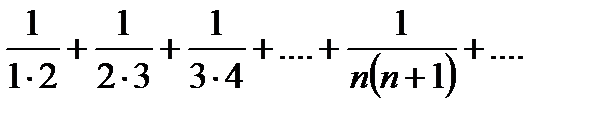
Решение. Напишем частичную сумму заданного ряда

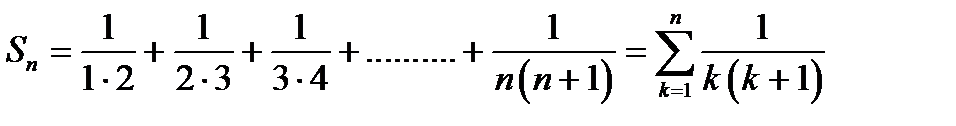
Каждое из слагаемых представим в виде суммы простейших так, как это делали в интегралах

 

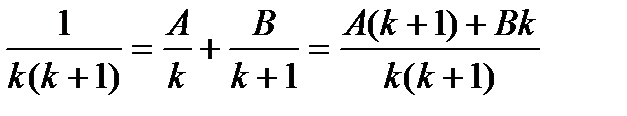
Числители выражений слева и справа равны, подставляя в равенство корни знаменателя, найдем А и В

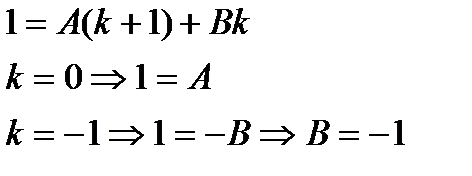
то есть

.

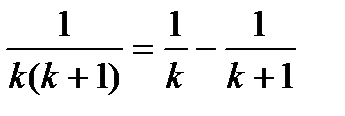Применим формулу к каждому члену частичной суммы ряда

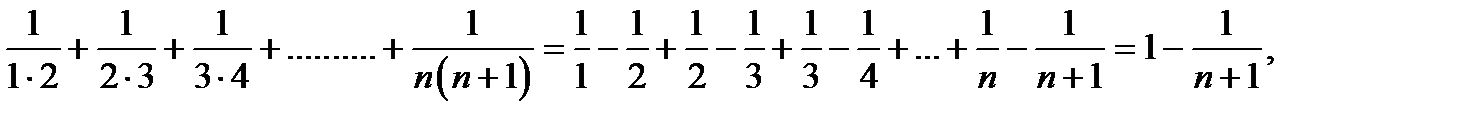
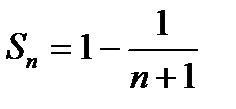
Рассмотрим предел частичных сумм

 

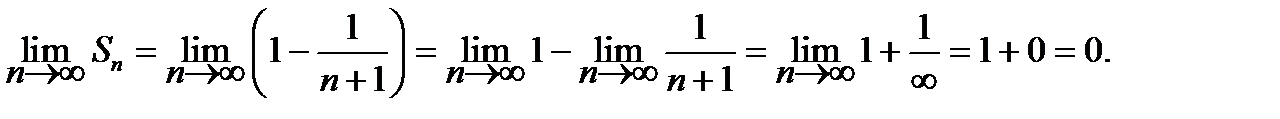
Следовательно, ряд сходится и его сумма равна 1.

Пример 2. Дан числовой ряд

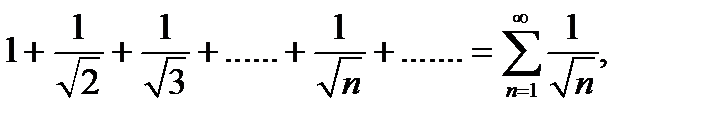
исследовать сходимость ряда.

Решение. Заменим в частичной сумме каждое слагаемое на последнее 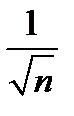, тем самым уменьшим частичную сумму

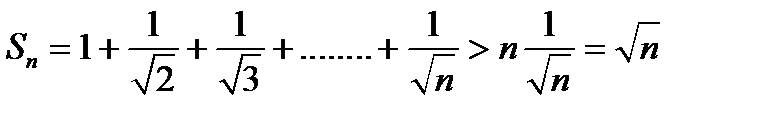
Величина 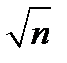 бесконечно возрастает с ростом n. Поэтому предел последовательности S_n при n ® ¥ равен бесконечности и ряд расходится.

Пример 3. Определить сходимость следующего ряда:

 

1 - 1 + 1 - 1 + (-1) ^{n +1} +....

 

Решение. Четная частичная сумма этого ряда S _{2 n} = 0, а нечетная - S _{2 n +1} = 1. Это означает, что предел 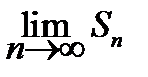не существует. Следовательно, данный ряд расходится.

Теорема о необходимом условии (признаке) сходимости числового ряда. Если числовой ряд сходится, то его общий член при n ® ¥ стремится к нулю, т.е.

 

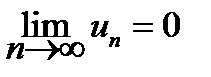                                                                                                   (7.3)

 

Доказательство. Рассмотрим две соседние частичные суммы ряда (7.2)

 

S_{n- 1} = u ₁ + u ₂ + u ₃ +... u_{n- 1},

S_n = u ₁ + u ₂ + u ₃ +... u _{n -1} + u_n = S_{n- 1} + u_n.

Из сходимости ряда следует, что

 

 

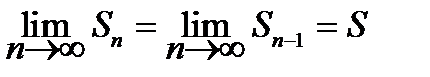
С другой стороны, по теоремам о пределах,

 

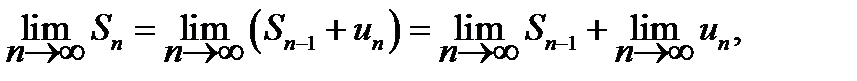
т. е.

S = S +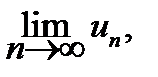

откуда и следует (7.2) .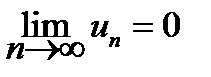

Введенное условие сходимости является лишь необходимым, но не достаточным. Это означает, что существуют расходящиеся ряды, у которых

.

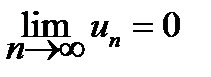Пример. Ряд, рассмотренный в примере 2

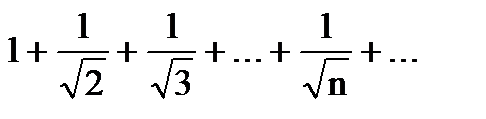
Расходится, но его общий член стремится к нулю. Действительно

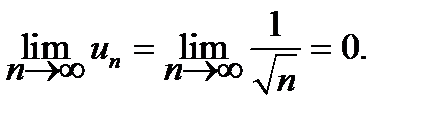
Аналогичным свойством обладает гармонический ряд, который будет рассмотрен ниже.