Знакочередующиеся ряды

 

Знакочередующимися рядами называются ряды вида

 

u ₁ - u ₂ + u ₃  - ... + (-1) ^{n +1} u_n  +...                                                           (7.17)

 

где все u_n > 0.

 

Сходимость таких рядов исследуется по теореме Лейбница: если в знакочередующемся ряде (7.17) все члены таковы, что u ₁ > u ₂  > …> u _n >.... и , то ряд (7.17) сходится, его сумма положительна и не превосходит первого члена ряда u ₁.

Доказательство. Возьмем сумму четного числа первых членов S _{2 m ,} которая положительна.

 

S _{2 m} = (u ₁ - u ₂ ) + (u ₃ - u ₄ ) +......+ (u _{2 m -1} – u _{2 m} ) > 0,  

 

так как выражение в каждой скобке больше нуля. S _{2 m} возрастает при росте m, т.к. S _{2 m} = S _{2(m -1)} + (u _{2 m -1} – u _{2 m} ) > S _{2(m -1)}.

С другой стороны

 

S _{2 m} = u ₁ - (u ₂  - u ₃ )  - (u ₄ – u ₅)......- (u _{2 m -2} - u _{2 m -1}) – u _{2 m} < u ₁.

 

т. е. при росте m S _{2 m} возрастает и ограничена сверху. Следовательно, имеет предел S = 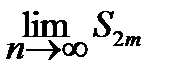 . Нечетные суммы будут иметь тот же предел. Действительно 

S _{2 m +1} = S _{2 m} + u _{2 m +1}

  

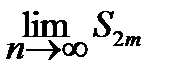   +  = S + 0 = S.

 

Четные и нечетные суммы ряда имеют тот же предел, следовательно, ряд сходится. Теорема доказана.

По знакочередующемуся ряду можно построить соответствующий ему положительный ряд u ₁ + u ₂  + u ₃ + u ₄ + …+ u_n +.... Если такой положительный ряд сходится, то знакочередующийся ряд называют абсолютно сходящимся, в противном случае ряд называют условно сходящимся. В абсолютно сходящемся ряде члены ряда можно переставлять без потери сходимости, в условно сходящемся ряде перестановка членов ряда запрещена, т.к. она может привести к потере сходимости. 

 

                                      

 7.2. Степенные ряды

 

Степенным рядом  по степеням x называется функциональный ряд вида

 

C ₀ + C ₁ x + C ₂ x ² +... C_nxⁿ +... = 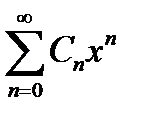,                                          (7.18)

где C ₀, C ₁,... C_n,... не зависят от переменной x и называются коэффициентами этого ряда.

Если при x = x ₀ числовой ряд сходится, то x ₀ называется точкой сходимости ряда (7.18). Областью сходимости  ряда называется множество всех точек сходимости этого ряда.

Степенной ряд (7.18) всегда сходится, по крайней мере, в точке x = 0.

 

Степенной ряд (7.18) сходится в точке x ₀ абсолютно, если сходится ряд образованный из модулей членов числового ряда

 

½ C ₀½ + ½ C ₁x₀½ + ½ C ₂ x ₀²½ +... ½ C_n x ₀ ⁿ ½ +....                        (7.19)

 

Найдем область сходимости ряда (7.18), используя признак Даламбера

для положительных числовых рядов. По этому признаку ряд (7.19) сходится, если

 

Следовательно, по признаку Даламбера ряд (4.54) заведомо сходится при

 

 и расходится при .

 

Величина  

                                                                                  (7.20)

называется радиусом сходимости  ряда степенного ряда. Ряд заведомо сходится в интервале ½ x ½ < R или - R < x < R, который называется интервалом сходимости.

Признак Даламбера ничего не говорит о сходимости ряда в точках х = В этих точках сходимость ряда исследовать отдельно.

Исследовать степенной ряд на сходимость означает найти его интервал сходимости и установить сходимость или расходимость ряда в граничных точках интервала, т.е. при x = R и x = - R.

Пример. Исследовать на сходимость степенной ряд

Решение. Используя формулу (7.20), имеем

Интервал сходимости данного ряда характеризуется неравенством ½ x ½ < 2. Исследуем сходимость ряда в граничных точках x = ±2. Очевидно, что

.

Оба эти ряда расходятся, так как не выполняется необходимое условие сходимости численных рядов. Следовательно, область сходимости данного степенного ряда совпадает с интервалом сходимости.

Пример. Найти область сходимости следующего ряда

1 + x + 2² x ²  + 3³ x ³ +... + nⁿxⁿ  +... = 1 + .

Решение. По формуле (7.20) найдем

.

 

Следовательно, ряд сходится только в одной точке x = 0.

Пример. Найти область сходимости следующего ряда:

 

.

 

Решение. Так как

 

 

то ряд сходится при всех конечных значениях x, т.е. -¥ < x <¥.