Рис.1.32. График решения жесткой системы

Решение дифференциальных уравнений высших порядков. Если в уравнении есть производные высших порядков, то действуем, преобразуя уравнение с понижением степени производной, но с увеличением числа переменных. Решим краевую задачу. d²x/dt²+4dx/dt+13x=e^sin^t

при x(0.25)=-1, x^/(0.25)=1 на интервале [0.25; 2].

Преобразуем следующим образом. Пусть y=dx/dt. Тогда получим систему уравнений.

dy/dt=-4y-13x+e^{sin t} dx/dt=y

с начальными условиями y(0.25)=1, x(0.25)=-1;

опишем ее в функции exSistVP.

function f=exSistVP(t,x) f=[-4*x(1)-13*x(2)+exp(sin(t)); x(1)]; end

Для ее решения воспользуемся функцией ode45.

function Start_difur2 x0=[1;-1]; [T, X]=ode45(@exSistVP,[0.25 2], x0); plot(T, X(:,1),'r-',T,X(:,2),'g-') end

Ей передадим имя М-функции для вышеописанной системы, интервал изменения параметра Т, вектор х0 начальных условий для переменных

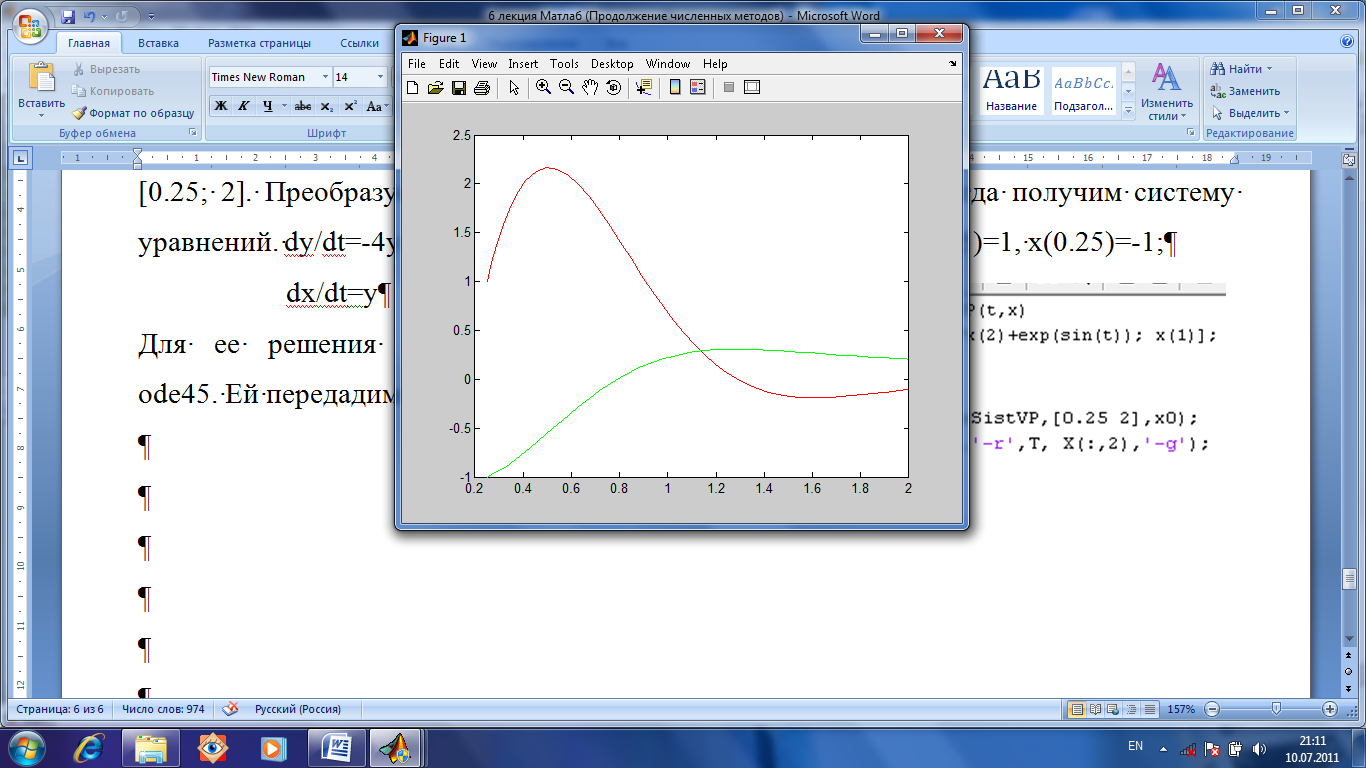
Функция ode45 вернет нам матрицу для Х и вектор для Т. Построим (рис.1.33) график.

Рис.1.33. Решение диф. уравнения высших порядков.

Обработка результатов эксперимента. Построение полиномиальной зависимости. Для этого есть функция polyfit, которой передаются массив абсцисс, массив ординат (экспериментальных точек) и степень полинома, который требуется получить так, чтобы он описывал экспериментальную зависимость массива ординат от массива абсцисс. Функция возвращает вектор коэффициентов вышеупомянутого полинома.

function Start_poly10 x=[0 4 10 15 21 29 36 51 68]; y=[66.7 71.0 76.3 80.6 85.7 92.9 99.4 113.6 125.1]; [a]=polyfit(x,y,1) xmas=0:0.1:68; ymas=a(1)*xmas+a(2); % для графика plot(x,y,'o',xmas,ymas,'-r'); end

%коэффициенты %полинома a = 0.8706 67.5078

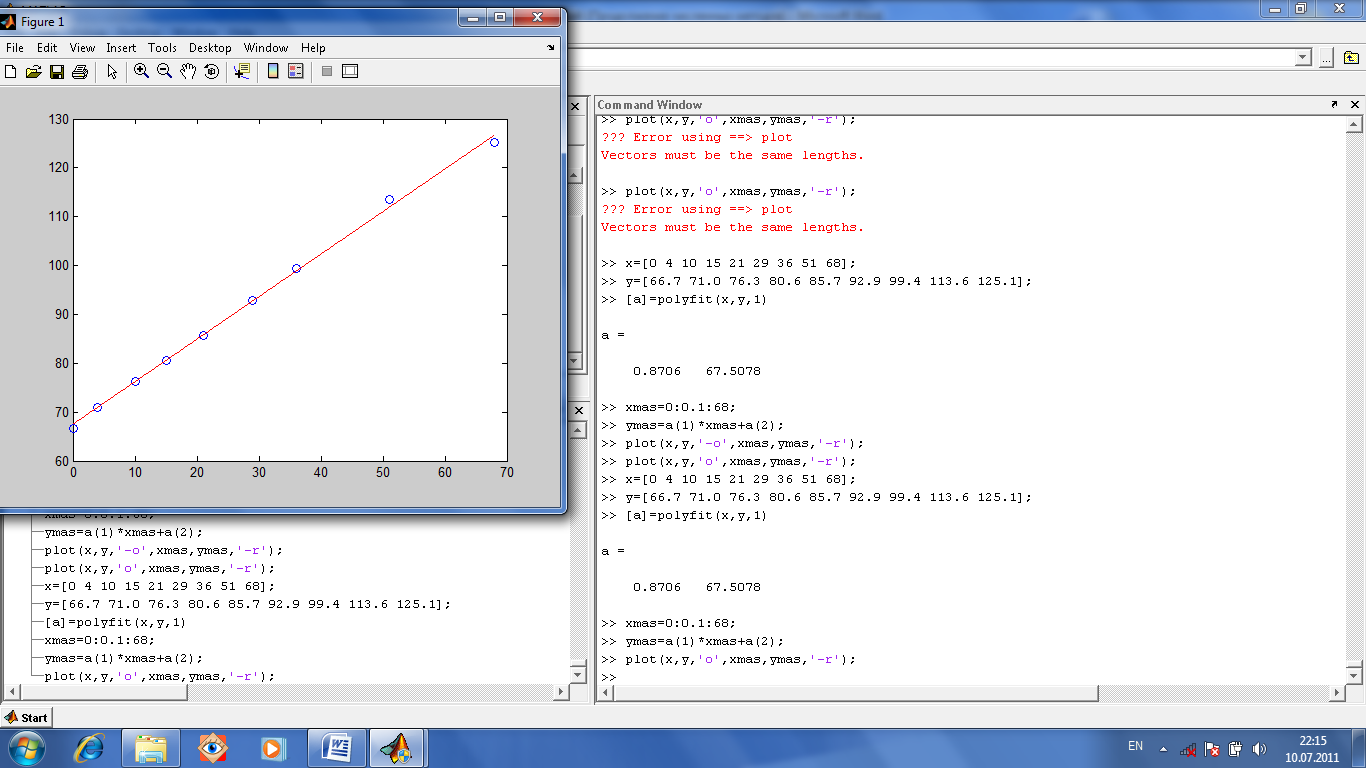
Будет построен график (рис.1.34),на котором можно будет сравнить исходные точки и расчетный график. Расчетный график построен по коэффициентам полинома.