Рис.1.36. В зависимости от используемых методов, получаются различные расчетные результаты

function Start_interp1

x=[0.43 0.48 0.55 0.62 0.7 0.75];

y=[1.6359 1.73234 1.87686 2.03345 2.22846 2.35973];

n=length(x);

t=[0.45 0.52 0.59 0.67 0.72];

xi=[x(1):0.02:x(length(x))];

yiN=interp1(x,y,xi,'nearest');

yiL=interp1(x,y,xi,'linear');

yiS=interp1(x,y,xi,'spline');

yTS=interp1(x,y,t,'spline');

yTN=interp1(x,y,t,'nearest');

yTL=interp1(x,y,t,'linear');

plot(x,y,'o',xi,yiN,'r-',xi,yiL,'g-',xi,yiS,'c-',t,yTN,'x',t,yTL,'*',t,yTS,'+');

grid on;

end

linear линейная интерполяция;

spline кубический сплайн;

nearest интерполяция по соседним точкам (значение равно значению в ближайшей узловой точке).

Подбор параметров. Для подбора параметров предназначена функция [res]=lsqcurvefit(fun, a0, x, y, Lx, Rx), где fun имя М-функции, вычисляющей левую часть выражения вида y=f(x, a₀, a₁, …, a_k), параметры которой a₀, a₁, …, a_k неизвестны и их-то и надо найти. Они перечислены в векторе возвращаемых значений res. а0 начальное приближение параметров. x, y экспериментальные данные. Lx, Rx ограничения на параметры вида Lx≤x≤Rx, Lx≤x, x≤Rx.

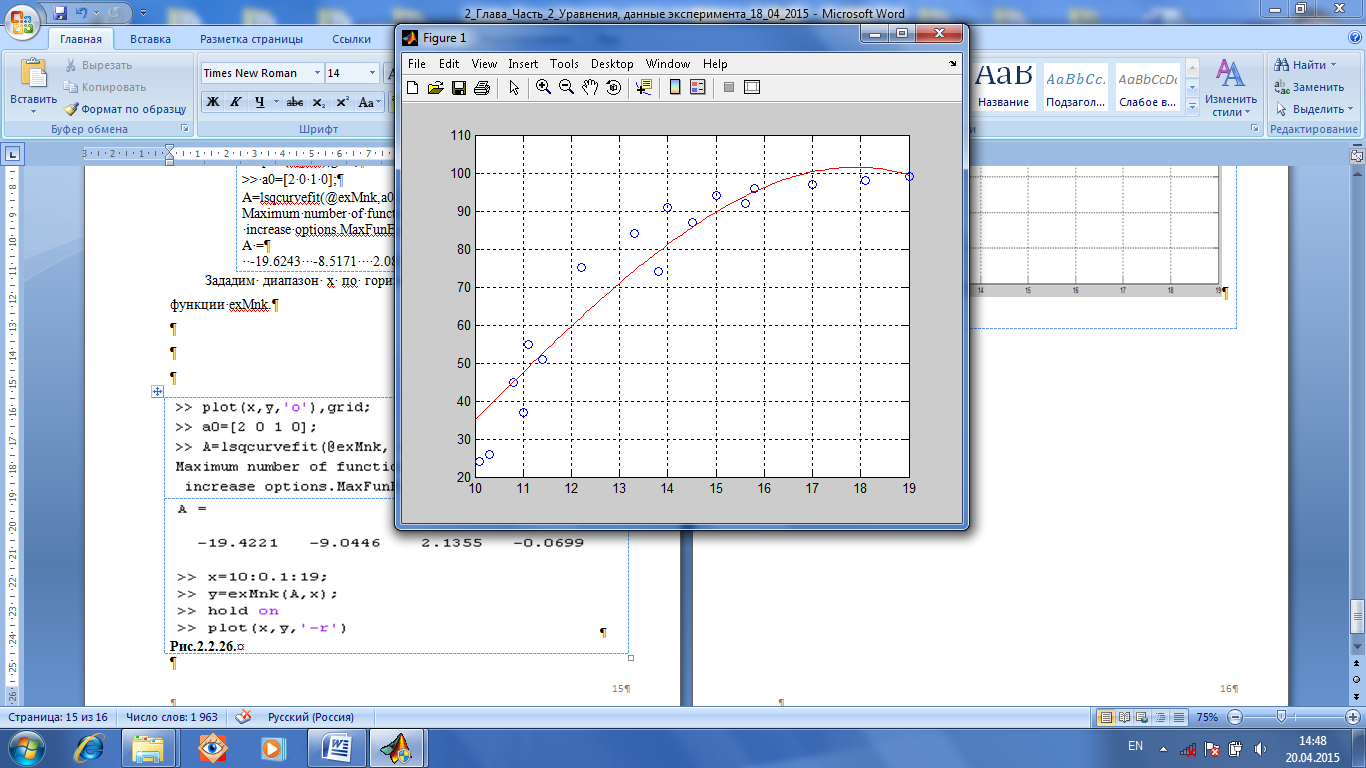
Пусть, для примера (Рис.1.37), надо подобрать параметры функции y=a₁+a₂x+a₃x²+a₄x³. Пусть даны экспериментальные данные.

Х	10.1	10.3	10.8	11	11.1	11.4	12.2	13.3	13.8	14	14.5	15	15.6	15.8	17	18.1	19
У	24	26	45	37	55	51	75	84	74	91	87	94	92	96	97	98	99

Выберем вектор начальных приближений а0=(2, 0, 1,0).

Опишем функцию exMnk, она вычисляет значение многочлена

function y=exMnk(a,x) y=a(1)+a(2)*x+a(3)*x.^2+a(4)*x.^3; end

Затем введем данные и построим график по ним.

>> X=[10.1,10.3,10.8,11,11.1,11.4,12.2,13.3,13.8,14,14.5,15,15.6,15.8,17,18.1,19]; >> Y=[24, 26, 45, 37, 55, 51, 75, 84, 74, 91, 87, 94, 92, 96, 97, 98, 99];

Применим функцию lsqcurvefit(@exMNK,a0,x,y), получим коэффициенты полинома.

>> plot(x,y,'o'),grid; >> a0=[2 0 1 0]; A=lsqcurvefit(@exMnk,a0,X,Y)		Maximum number of function evaluations exceeded; increase options.MaxFunEvals A = -19.6243 -8.5171 2.0875 -0.0689
function Start_lsq x=10:0.1:19; y=exMnk(A,x); plot(X,Y,'o'),grid; hold on; plot(x,y,'r-'); end	Зададим диапазон х по горизонтальной оси и построим (рис.1.37) график функции exMnk.

Рис.1.37. Экспериментальные данные и расчетный график.

Поиск экстремума функции одной переменной. При решении задач поиска максимума (минимума) выделяют локальный (с указанием границ) и глобальный максимум (минимум). Поиск (локального (в пределах определенного интервала) минимума осуществляет функция [x,y]=fminbnd(имяФункции,границыИнтервала).

Если же надо найти локальный максимум, то исследуемую функцию берут с другим знаком и ищут ее минимум, который фактически является ее максимумом. При этом значение функции в максимуме это найденное значение с другим знаком.

Локальный минимум функции одной переменной ищет встроенная функция [x, y]=fminbnd(name, a, b, options). В ней:

· name имя М-функции,

· a, b границы поиска,

· options параметры управляющие ходом решения,

· x, y координаты точки минимума.

Для вычисления локального максимума, надо взять функцию name с другим знаком. Для примера, рассмотрим функцию y(x)=x⁴-0.5x³-28x²+140

Сначала найдем минимум на интервале, например, от -4 до -2.

[x,y]=fminbnd(@ext,-4,-2), где @ext обращение к М-функции вычисляющей интересующую нас функцию.

Потом найдем максимум на интервале от -6 до 6, для этого обратимся не к @ext, а к @ext_2, в которой функция y(x) взята с другим знаком, то есть y(x)=-(x⁴-0.5x³-28x²+140). То есть ее минимум будет максимумом исходной функции.

Получим и в том, и в другом случае координаты точки минимума (максимума) на заданном отрезке, что и требовалось.

function y=ext(x) y=x.^4-0.5*x.^3-28*x.^2+140; end function y=ext_2(x) y=-(x.^4-0.5*x.^3-28*x.^2+140); end function Start_fminb [x,y]=fminbnd(@ext,-6,6) [x,y]=fminbnd(@ext_2,-6,6) y=-y end

x = 3.9339 y = -84.2624 x = 5.0643e-006 y =  -140.0000 y = 140.0000

Минимальный шаг по аргументу

Если выбрано окончание процесса поиска экстремума (например, минимума) при условии, что последнее изменение аргумента стало меньше заданной минимальной величины, то это означает, что найденный ответ (то есть значение аргумента, при котором функция минимальна) указан с погрешностью, не превышающей заданную минимальную величину.