Рис. 1.28. Функция polyval обеспечивает графическое решение уравнения

Численное интегрирование. Для интегрирования существует очень много алгоритмов в современной вычислительной математике. Будем рассматривать выборочно некоторые из них.

Интегрирование методом трапеций означает, что подинтегральная площадка разбивается на трапециевидные подплощадки, границы между трапециями это вертикальные линии, проведенные через x₁, x₂, …, x_n равноотстоящие точки на оси Х, идущие от начала до конца интервала интегрирования [x₁ x_n]. Верхние границы трапеций это отрезки, соединяющие точки f(x₁), f(x₂), …, f(x_n). Нижние границы трапеций ось Х.

Для метода трапеций есть функция trapz(x,y).

При интегрировании методом Симпсона верхние границы подплощадок являются отрезками параболы. Для него есть функция quad(‘name’,a,b,tol,trace), где перечислены аргументы имя М-функции, левая и правая границы интегрирования, точность вычислений, а также параметр задающий таблицу с промежуточными точками результатами вычислений. Есть также весьма точный алгоритм Ньютона-Котеса 8-го порядка. Он вызывается функцией quad8(‘name’,a,b,tol,trace).

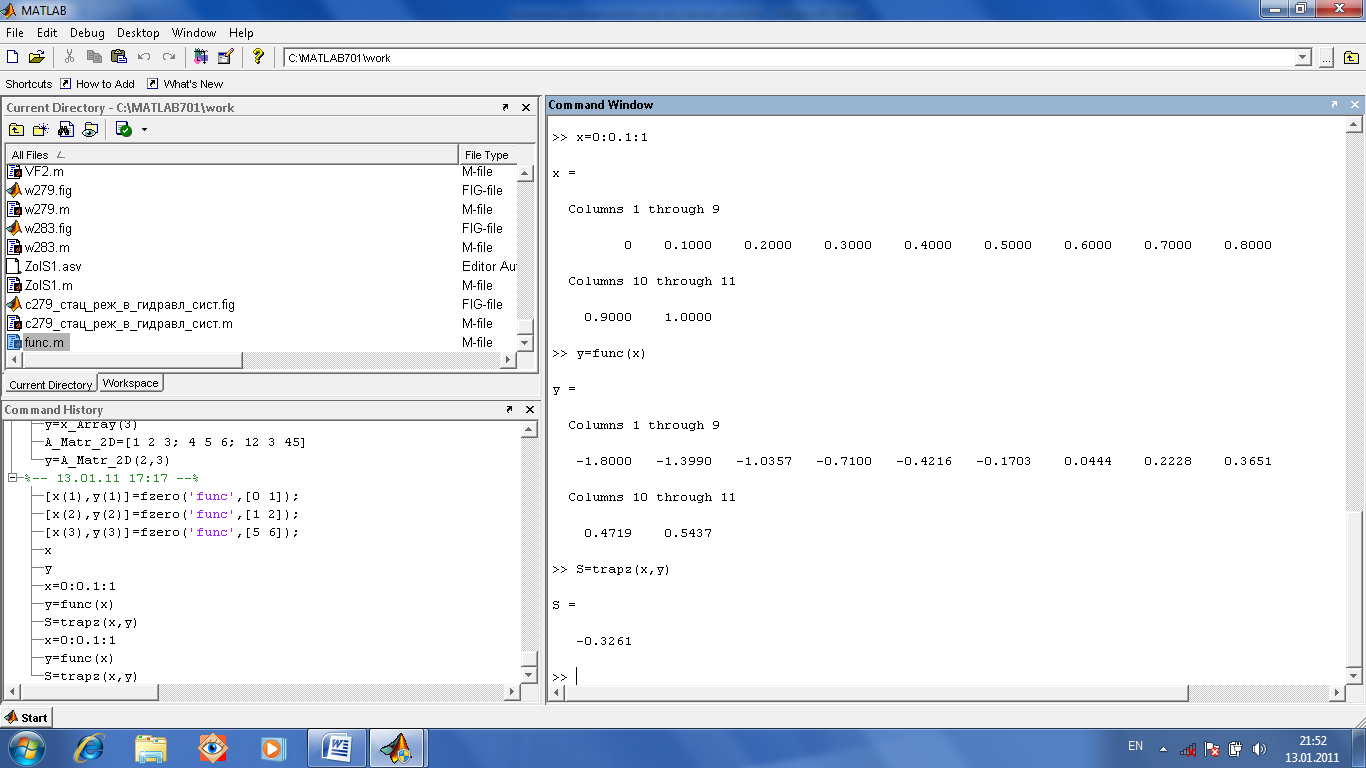
Пример решения определенного интеграла функцией trapz (методом трапеций) для вышеописанной функции func (см. рис.1.26), где для обработки вектора аргументов поставлена точка перед знаком возведения в степень y=0.2*exp(x) -2*(x-1).^2  при пределах интегрирования [0 1] с шагом разбиения 0,1 приведен на рис.1.29. Вполне очевидно, что с ростом числа точек разбиения по х (числа шагов, то есть при уменьшении шага по х) будет расти точность вычисления интеграла.