В соответствии с первой конкретной целью обучения по заданной теме – уметь определить целесообразность и необходимость расчета средних величин – необходимо решить следующую задачу.
Задача 1
Ниже приводится информация о длительности лечения в стационаре и исходах заболевания 45 больных пневмонией.
| Длительность лечения (дней) | Исходы заболевания |
| 25, 11, 12, 13, 24, 23, 23, 24,21 22, 21, 23, 22, 21, 14, 14, 22, 20, 20, 15, 15, 16, 20, 20, 16, 16, 20, 17, 17, 19, 19, 19, 18, 18, 18, 18, 19, 19, 17, 17, 18, 18, 19, 26 | выздоровление – 23 чел. улучшение – 13 чел. без перемен – 7 чел. ухудшение – 1 чел. летальность – 1 чел. |
Задания:
1. Укажите характер вариации представленных данных и объясните, почему Вы так считаете.
2. Определите целесообразность и необходимость расчета средних величин.
Ответ:
1) Учитывая, что изучаемый нами варьирующий признак, а именно длительность лечения больных пневмонией, имеет количественное выражение, представленная вариация называется количественной, а ряд распределения – вариационным, он и будет основанием для расчета средней величины.
2) Информация об исходах заболевания пневмонией не имеет количественной меры (выздоровление, улучшение и т.д.), вариация будет называться качественной, а ряд распределения – атрибутивным, средняя величина в этом случае не рассчитывается, но, анализируя данные такого ряда, можно использовать моду.
3) Так как данные о длительности лечения в стационаре многочисленны и имеют количественное выражение, то рассчитывается средняя величина.
Если вы дали правильный ответ, приступайте к отработке следующих умений:
· Уметь построить вариационный ряд и рассчитать средние арифметические величины разными способами в зависимости от вида вариационного ряда;
· Уметь рассчитать показатели колеблемости вариационного ряда (изучаемого признака);
· Уметь оценить полученные данные и сделать выводы.
Для этого решите следующие задачи:
Задача 2
На 8 лекциях по социальной медицине и организации здравоохранения в весеннем семестре на одном из потоков IV курса лечебного факультета присутствовало студентов: 174, 168, 175, 158, 172, 174, 171, 155, 169.
Задания:
1. Постройте вариационный ряд и определите его вид (ответ обоснуйте).
2. Рассчитайте среднюю арифметическую величину, моду, медиану.
3. Определите показатели колеблемости вариационного ряда (лимиты, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
4. Оцените полученные данные и сделайте вывод.
Ответ:
1. Чтобы построить вариационный ряд, необходимо расположить варианты в возрастающем порядке (графа 1, табл. 2.1).
Таблица 2.1
Распределение студентов IV курса лечебного факультета,
присутствовавших на лекциях
| Число студентов, V | Число лекций, р | d | d2 |
| 1 | 2 | 3 | 4 |
| 155 158 168 169 171 172 174 175 | 1 1 1 1 1 1 1 1 | -13 -10 0 +1 +3 +4 +6 +7 | 169 100 0 1 9 16 36 49 |
| ΣV=1343 | Σр=n=8 | Σ d2=380 |
2. Построенный вариационный ряд – дискретный или прерывистый, т.к. варианты отличаются друг от друга на целое число и не имеют промежуточных дробных значений.
3. Вариационный ряд – простой, т.к. каждая варианта встречается только один раз, т.е. р=1 (графа 2, табл. 2.1).
4. Так как вариационный ряд простой, необходимо рассчитать простую среднеарифметическую величину по формуле: 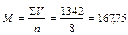 ≈168 студентов.
≈168 студентов.
5. Моду (Мо) рассчитать нельзя, т.к. р=1.
6. Медиана (Ме) рассчитана с учетом центральных вариант. Центральными вариантами являются 4-ая и 5-ая варианты (169 и 171). 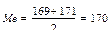 студентов.
студентов.
7. Lim=175÷ 155 студентов; Am= 175 – 155= 20 студентов. Для расчета среднего квадратического отклонения (δ) определены истинные отклонения (d) вариант от истинной средней арифметической и заполнены графы 3, 4 табл. 2.1 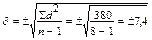 студентов.
студентов.
δ по Ермолаеву = 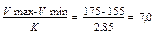 студентов.
студентов.
СV= 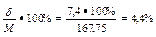 .
.
Выводы:
1. Вариационный ряд – дискретный, простой.
2. На лекциях по социальной медицине в весеннем семестре присутствовало в среднем 168 студентов IV курса лечебного факультета.
3. Средняя арифметическая величина является характерной, типичной для данного вариационного ряда, т.к. в пределах 153,2 – 182,8 (М±2δ) находятся все варианты вариационного ряда, а достаточно 95%.
4. Степень колеблемости вариационного ряда малая по коэффициенту вариации.
Задача 3
Сроки стационарного лечения 30 больных детей (в днях): 17, 7, 16, 18, 12, 12, 14, 14, 17, 18, 15, 18, 19, 17, 15, 15, 15, 17, 16, 9, 10, 10, 11, 16, 19, 20, 16, 17, 15, 15.
Задания.
1. Постройте вариационный ряд и определите его вид (ответ обоснуйте).
2. Рассчитайте среднюю арифметическую величину, моду, медиану.
3. Определите показатели колеблемости вариационного ряда (лимит, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
4. Оцените полученные данные и сделайте выводы.
Ответ.
1. Для построения вариационного ряда варианты были расположены в возрастающем порядке (графа 1, табл. 3.1).
Таблица 3.1
Распределение больных детей по срокам
стационарного лечения
| Сроки стационарного лечения (в днях), V | Число больных р | Vр | d | d2 | d2р |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 9 10 11 12 14 15 16 17 18 19 20 | 1 1 2 1 2 3 6 4 4 3 2 1 | 7 9 20 11 24 42 90 64 68 54 38 20 | -8 -6 -5 -4 -3 -1 0 +1 +2 +3 +4 +5 | 64 36 25 16 9 1 0 1 4 9 16 25 | 64 36 50 16 18 3 0 4 16 27 32 25 |
| Σр=n=30 | ΣVр=447 | Σd2p=291 |
2. Построенный вариационный ряд – дискретный или прерывистый, т.к. варианты отличаются друг от друга на целое число и не имеют промежуточных, дробных значений. Вариационный ряд – взвешенный, т.к. одна и та же варианта повторяется несколько раз, варианты как бы взвешиваются по числу соответствующих им частот – р>1 (графа 2, табл. 3.1).
3. Учитывая, что вариационный ряд взвешенный, была рассчитана взвешенная среднеарифметическая величина по формуле: 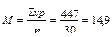 дней.
дней.
4. Мода (Мо) – рассчитывалась как наиболее часто встречающаяся варианта, чаще всего (6 раз) встречались дети со сроком стационарного лечения 15 дней. Следовательно, Мо=15 дней.
5. Число наблюдений в данной задаче четное, поэтому медиана (Ме) рассчитывалась следующим образом: 30: 2 = 15, т.е. медиана соответствует 15-й по счету варианте, это варианта – 15 дней. Следовательно, Ме=15 дней.
6. Lim=20÷7; Am=13. Для расчета среднего квадратического отклонения определялись истинные отклонения вариант от истинной среднеарифметической величины (d) и заполнялись графы 4, 5, 6 табл. 3.1).
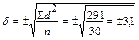 дней.
дней.
δ по Ермолаеву = 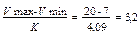 дней.
дней.
СV= 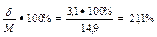 .
.
7. Выводы.
· Вариационный ряд – дискретный, взвешенный.
· Мо=Ме≈М, что характерно для нормального распределения.
· Сроки стационарного лечения больных детей составляет в среднем 14,9≈15 дней.
· Средняя арифметическая величина является типичной для данного вариационного ряда, т.к. в пределах М±2δ находится около 97% вариант вариационного ряда.
· Степень колеблемости вариационного ряда сильная по коэффициенту вариации, вместе с тем мы не можем говорить о ненадежности средней арифметической, т.к. СV<40%.
Задача 4
Число состоящих на диспансерном учете больных с гипертонической болезнью у 50 участковых терапевтов города: 20, 21, 22, 23, 25, 25, 26, 27, 27, 25, 26, 27, 25, 22, 23, 24, 39, 23, 40, 22, 26, 30, 24, 26, 24, 25, 24, 25, 24, 28, 24, 29, 25, 26, 27, 27, 30, 31, 34, 31, 35, 32, 30, 30, 36, 25, 35, 38, 39, 28.
Задания.
1. Постройте вариационный ряд и определите его вид (ответ обоснуйте).
2. Рассчитайте среднюю арифметическую величину, моду, медиану.
3. Определите показатели колеблемости вариационного ряда (лимит, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
4. Оцените полученные данные и сделайте выводы.
Ответ.
1. Чтобы построить вариационный ряд, расположим варианты в возрастающем порядке (графа 1, табл. 4.1).
2. Построенный первоначальный ряд – дискретный, т.к. варианты отличаются друг от друга на целое число и взвешенный, т.к. варианты повторяются несколько раз (графа 2, табл. 4.1). Учитывая, что число наблюдений равно 50 (n>30), и для облегчения расчетов из первоначального ряда построим сгруппированный вариационный ряд с соответствующими частотами (графы 3, 4, табл. 4.1). Величина интервала (i) для сгруппированного ряда рассчитывалась по формуле: 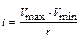 , где r – число предполагаемых групп (см. табл. 2).
, где r – число предполагаемых групп (см. табл. 2).  ≈ 2 больных.
≈ 2 больных.
Таблица 4.1
Распределение больных гипертонической болезнью,
состоящих на диспансерном учете у участковых терапевтов
| Первоначальный ряд | Сгруппированный ряд | |||||||
| Число больных, состоящих на диспанс. учете, V | Число участковых терапевтов, р | Число больных, состоящих на диспан. учете, V | Число участковых терапевтов, р | V | р | а | ар | а2р |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | 1 1 3 3 6 8 5 5 2 1 4 2 1 0 1 2 1 0 1 2 1 | 20 – 21 22 – 23 24 – 25 26 – 27 28 – 29 30 – 31 32 – 33 34 – 35 36 – 37 38 – 39 40 – 41 | 2 6 14 10 3 6 1 3 1 3 1 | 21 23 25 27 29 31 33 35 37 39 41 | 2 6 14 10 3 6 1 3 1 3 1 | -2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 | 4 6 0 10 6 18 4 15 6 21 8 | 8 6 0 10 12 54 16 75 36 147 64 |
| ∑р=n=50 | ∑р=n=50 | n=50 | ∑ар=98 | ∑а2р=428 | ||||
Так как вариационный ряд взвешенный, рассчитываем взвешенную среднюю арифметическую с использование способа моментов, т.к. число наблюдений n>30.
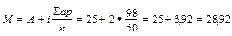 больных.
больных.
Величина интервала (i) вводится в формулу определения М и δ в том случае, если в графе 7 «условные отклонения» – а определяются не как разность между вариантами и условными средними (V – А), а даются условные обозначения –1, -2, 0, +1, +2 и т.д., предполагающие, что разность между центральными вариантами равна 1. Мо=25 больных; Ме=26 больных.
3. Lim=40 ÷ 20; Am=20.

δ по Ермолаеву = 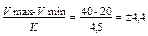 больных.
больных.
СV= 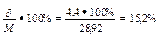 .
.
Выводы.
1. Вариационный ряд – дискретный, взвешенный, сгруппированный.
2. Мо=25 больных; Ме=26 больных.
3. Lim=40 ÷ 20; Am=20.
4. У участковых терапевтов на диспансерном учете состоит в среднем 28,9≈29 больных.
5. Средняя арифметическая величина является типичной для данного вариационного ряда, т.к. в пределах М±2δ (20,5 ÷ 37,7) находится 95% вариант вариационного ряда.
6. Степень колеблемости вариационного ряда средняя (по коэффициенту вариации).
Задача 5
Результаты измерения роста у мальчиков 10 лет, обучающихся в школах-интернатах (в см): 127,0; 126,5; 128,0; 120,0; 123,0; 121,0; 126,0; 123,5; 122,0; 127,0; 123,0; 122,5; 127,0; 126,0; 128,5; 124,5; 127,0; 125,5; 125,5; 128,0; 125,0; 127,0; 130,0; 123,5 128,0; 126,0; 124,5; 127,0; 123,5; 127,0; 130,0; 126,5; 126,0; 128,0; 124,5; 127,0; 125,0; 124,5; 128,0; 128,5; 125,5; 128,0; 127,0; 126,0; 126,5; 131,0; 127,0; 127,0; 131,0; 126,0; 128,0; 124,5; 125,0; 127,0; 130,5; 125,0; 127,0; 124,5; 126,0; 128,5 125,0; 128,0; 126,5; 130,0; 125,5; 128,5, 126,0; 126,0; 130,5; 124,5; 128,0; 125,5; 125,0; 128,0; 125,5; 126,0; 124,0; 131,0; 125,5; 130,5; 129,5; 127,0; 128,5 126,5; 130,0; 130,0; 127,0; 127,0; 127,0; 127,0; 128,0; 128,0; 129,0; 129,0; 129,0; 134,5; 130,5; 132,0; 132,0; 133.
Задания.
1. Постройте вариационный ряд и определите его вид (ответ обоснуйте).
2. Рассчитайте среднюю арифметическую величину, моду, медиану.
3. Определите показатели колеблемости вариационного ряда (лимит, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
4. Оцените полученные данные и сделайте выводы.
Ответ.
1. Чтобы построить вариационный ряд, расположим варианты в возрастающем порядке (графа 1, табл. 5.1).
2. Построенный первоначальный ряд – непрерывный, т.к. варианты имеют промежуточные, дробные значения, и взвешенный, т.к. одна и та же варианта встречается несколько раз (графа 2, табл. 5.1). Так как число наблюдений большое (n=100), для облегчения расчетов из первоначального ряда построим сгруппированный вариационный ряд с соответствующими группам частотами (графы 3, 4, табл. 5.1).
Таблица 5.1
Распределение мальчиков по росту (в см)
| Первоначальный ряд | Сгруппированный ряд | |||||||
| Рост, V | Число мальчиков, р | Рост, V | Число мальчиков, р | V | р | а | ар | а2р |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 120,0 121,0 122,0 122,5 123,0 123,5 124,5 125,0 125,5 126,0 126,5 127,0 128,0 128,5 129,0 129,5 130,0 130,5 131,0 132,0 133,0 134,5 | 1 1 1 1 2 3 8 6 7 10 5 18 12 5 3 1 5 4 3 2 1 1 | 120,0 – 121,9 122,0 – 123,9 124,0 – 125,9 126,0 – 127,9 128,0 – 129,9 130,0 – 131,9 132,0 – 133,9 134,0 – 135,9 | 2 7 21 33 21 12 3 1 | 121,0 123,0 125,0 127,0 129,0 131,0 133,0 135,0 | 2 7 21 33 21 12 3 1 | -6 -4 -2 0 +2 +4 +6 +8 | -12 -28 -42 0 +42 +48 +18 +8 | 72 112 84 0 84 192 108 64 |
| ∑р=n =100 | ∑р=n =100 | n=100 | ∑ар =34 | ∑а2р =716 | ||||
3. Величина интервала (i) для сгруппированного ряда рассчитывалась по формуле: 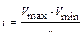 , где r – число предполагаемых групп (см. табл. 2).
, где r – число предполагаемых групп (см. табл. 2).
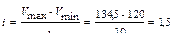 ≈ 2 см
≈ 2 см
Так как вариационный ряд взвешенный, рассчитываем взвешенную среднюю арифметическую. Учитывая, что число наблюдений большое, используем способ моментов:
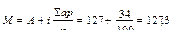 см
см
Величина интервала (i) не введена в формулы определения М и δ, т.к. условное отклонение – а определялось как разность (V – А), где А – условная средняя, наиболее часто встречающаяся варианта.
4. Lim=134,5 ÷ 120,0: Am=14,5.

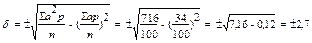 см
см
δ по Ермолаеву = 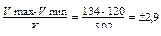 см.
см.
СV=  .
.
Выводы.
1. Вариационный ряд – непрерывный, взвешенный, сгруппированный.
2. Мо=Ме=М, что характерно для нормального распределения.
3. Lim=134,5 ÷ 120,0; Am=14,5.
4. Средний рост мальчиков 10 лет, обучающихся в школах-интернатах, составляет 127,3 см.
5. Средняя арифметическая величина является типичной для данного вариационного ряда, т.к. в пределах 116,5 – 138,1 см (М±2δ) находятся все варианты вариационного ряда.
6. Степень колеблемости ряда слабая (СV<10%).
Приложение 1
Граф логической структуры темы: «Средние величины, их использование в здравоохранении»

 Ι ΙΙ
Ι ΙΙ












Приложение 2
Логическая структура темы: «Средние величины, их использование в здравоохранении»
(фрагмент темы: «Расчет средних величин»)

Приложение 3
Логическая структура темы "Средние величины, их использование в здравоохранении"
(фрагмент темы "Расчет показателей колеблемости вариационного ряда")
 | |||
 | |||


Приложение 4
Алгоритм статистической обработки медицинских данных с помощью средних величин

Приложение 5
Алгоритм расчета параметров взвешенного вариационного ряда
| 1. | Построить взвешенный вариационный ряд, расположив все варианты (V) в возрастающем или убывающем порядке с соответствующими им частотами (р), графа 1 и 2. |
| 2. | Перемножить каждую варианту на соответствующую частоту (Vр), найти их сумму (∑Vр), графа 3. |
| 3. | Рассчитать среднюю арифметическую взвешенную (М). |
| 4. | Найти истинные отклонения d = V – M, графа 4. |
| 5. | Возвести каждое истинное отклонение в квадрат d 2, графа 5. |
| 6. | Найти произведение d2×р, по всем строкам ряда и определить их сумму ∑d2×р, графа 6. |
| 7. | Рассчитать среднее квадратическое отклонение (δ). |
| 8. | Определить ошибку репрезентативности (m). * |
| 9. | Рассчитать критерий достоверности (t). * |
| V | р | Vp | d (V–M) | d2 | d2p | Формулы для расчета |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
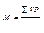
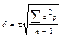 *
*  *
* 
| ||||||
| ∑р=n | ∑Vp | ∑d2p |
Примечание. * ошибка репрезентативности (m) и критерий достоверности (t) будут рассмотрены в следующей теме.
Приложение 6
Алгоритм расчета параметров взвешенного ряда по способу моментов
| 1. | Построить взвешенный вариационный ряд, расположив все варианты (V) в возрастающем или убывающем порядке с соответствующими им частотами (р), графа 1 и 2. |
| 2. | Выбрать условную среднюю (А) – можно взять любую варианту ряда, но желательно наиболее часто встречающуюся варианту. |
| 3. | Определить условное отклонение (а) каждой варианты от условной средней (а = V – А), графа 3. |
| 4. | Перемножить значение каждого условного отклонения на соответствующую частоту (aр), найти их сумму (∑aр), графа 4. |
| 5. | Найти истинную среднюю арифметическую взвешенную по способу моментов (М), формула 1. |
| 6. | Возвести каждое условное отклонение (а) в квадрат (а2), найти произведение (а2р) по всем строкам ряда и определить их сумму ∑a2р, графа 5, 6. |
| 7. | Рассчитать среднее квадратическое отклонение (δ) по способу моментов, формула 2. |
| 8. | Определить ошибку репрезентативности (m) *, формула 3. |
| 9. | Рассчитать критерий достоверности (t) *, формула 4. |
| V | р | A (V-A) | ap | a2 | a2p | Формулы для расчета |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
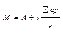 (1) (1)
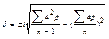 (2)
* (2)
* 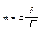 (3)
* (3)
*  (4) (4)
| ||||||
| ∑р=n | ∑ар | ∑a2p |
Примечание. * ошибка репрезентативности (m) и критерий достоверности (t) будут рассмотрены в следующей теме.
Приложение 7
Алгоритм расчета параметров сгруппированного ряда по способу моментов
| 1. | Построить сгруппированный вариационный ряд, определив число групповых вариант (не менее 5), величину интервала (i) по специальной таблице, середину, начало и конец групп вариант. Расположить группы вариант в возрастающем или убывающем порядке с соответствующими им частотами (р), графа 1 и 3. |
| 2. | Определить центральную варианту V (в непрерывных вариационных рядах как полусумму первых значений соседних групп, в дискретных вариационных рядах как полусумму крайних значений группы), графа 2 |
| 3. | Принять за единицу разность между соседними вариантами, введя в формулу для расчета средней арифметической величину интервала (i). |
| 4. | Выбрать условную среднюю А – можно взять любую варианту ряда, но желательно наиболее часто встречающуюся варианту. |
| 5. | Определить условное отклонение (а) каждой варианты от условной средней (а = V – А), графа 4. |
| 6. | Перемножить значение каждого условного отклонения (а) на соответствующую частоту (ар) и определить их сумму ∑aр, графа 5. |
| 7. | Найти истинную среднюю арифметическую взвешенную сгруппированного ряда по способу моментов (М), формула 1. |
| 8. | Возвести каждое условное отклонение (а) в квадрат (а2), найти произведение (а2р) по всем строкам ряда и определить их сумму ∑a2р, графа 6, 7. |
| 9. | Рассчитать среднее квадратическое отклонение (δ) по способу моментов, формула 2. |
| 10. | Определить ошибку репрезентативности (m) *, формула 3. |
| 11. | Рассчитать критерий достоверности (t) *, формула 4. |
| V | р | A (V-A) | ap | a2 | a2p | Формулы для расчета |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
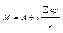 (1) (1)
 (2)
* (2)
* 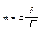 (3)
* (3)
*  (4) (4)
| ||||||
| ∑р=n | ∑ар | ∑a2p |
Примечание. * ошибка репрезентативности (m) и критерий достоверности (t) будут рассмотрены в следующей теме.
ТЕМА 4. МЕТОДИКА ОЦЕНКИ ДОСТОВЕРНОСТИ
 2020-10-10
2020-10-10 329
329








