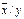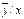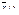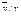2020-10-10
233
Построение эмпирических линий регрессии [ 30 мин. ]
Пример 1. Получены данные о длине листовой пластинки («х», мм) и диаметре штамба («у», см) у 31 сеянца алычи:
Длина листовой пластинки «х», мм и диаметр штамба «у», см у 31 сеянца алычи
| х | 76,6 | 72,2 | 67,0 | 66,5 | 63,3 | 65,4 | 63,9 | 63,1 | 63,0 | 62,5 | 62,2 |
| у | 4,56 | 4,79 | 4,49 | 4,32 | 4,59 | 4,32 | 4,67 | 4,29 | 4,57 | 4,20 | 4,12 |
| х | 61,0 | 60,2 | 60,0 | 59,6 | 59,5 | 58,9 | 58,0 | 57,8 | 57,6 | 57,0 | |
| у | 4,13 | 4,70 | 3,80 | 4,23 | 3,76 | 4,08 | 4,61 | 4,37 | 4,30 | 4,00 | |
| х | 56,8 | 55,4 | 55,0 | 53,8 | 53,7 | 52,0 | 51,4 | 51,0 | 50,9 | 48,5 | |
| у | 3,82 | 4,12 | 4,19 | 4,16 | 4,09 | 4,12 | 4,02 | 4,31 | 4,06 | 4,03 |
Строим корреляционную решетку: строки решетки – классы по признаку «у», ранжированные по убыванию середин сверху вниз; столбцы решетки – классы по признаку «х», ранжированные по убыванию середин слева направо. В программе Excel разносим пары значений признаков «х» и «у» по ячейкам решетки:
| Границы классов | Классы по «х» | Сумма по «у» |
| ||||||||
| 47,0-51,4 | 51,5-55,9 | 56,0-60,4 | 60,5-64,9 | 65,0-69,4 | 69,5-73,9 | 74,0-78,4 | |||||
| Середины классов | 49,2 | 53,7 | 58,2 | 62,7 | 67,2 | 71,7 | 76,2 | ||||
| Классы по «у» | 4,66-4,80 | 4,73 | 1 | 1 | 1 | 3 | 64,20 | ||||
| 4,51-4,65 | 4,58 | 1 | 2 | 1 | 4 | 64,70 | |||||
| 4,36-4,50 | 4,43 | 1 | 1 | 2 | 62,70 | ||||||
| 4,21-4,35 | 4,28 | 1 | 2 | 1 | 2 | 6 | 60,45 | ||||
| 4,06-4,20 | 4,13 | 1 | 5 | 1 | 3 | 10 | 56,40 | ||||
| 3,91-4,05 | 3,98 | 1 | 1 | 1 | 3 | 53,70 | |||||
| 3,76-3,90 | 3,83 | 3 | 3 | 58,20 | |||||||
| Сумма по «х» | 3 | 6 | 10 | 7 | 3 | 1 | 1 | 31 | |||
|
| 4,13 | 4,11 | 4,19 | 4,37 | 4,33 | 4,73 | 4,58 | ||||
2. Определяем координаты точек эмпирической линии регрессии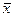 
/ у:
| у |
| 64,20 | 4,73 |
| 64,70 | 4,58 |
| 62,70 | 4,43 |
| 60,45 | 4,28 |
| 56,40 | 4,13 |
| 53,70 | 3,98 |
| 58,20 | 3,83 |
3. Определяем координаты точек эмпирической линии регрессии 
/ х:
| х |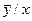 
|
| 49,2 | 4,13 |
| 53,7 | 4,11 |
| 58,2 | 4,19 |
| 62,7 | 4,37 |
| 67,2 | 4,33 |
| 71,7 | 4,73 |
| 76,2 | 4,58 |
4. Используя мастер диаграмм программы Excel, строим две сглаженные линии регрессии, определяем формат осей, добавляем два тренда
Эмпирические линии регрессии и тренды
Составление уравнений прямолинейной регрессии и построение теоретических линий регрессии [ 35 мин. ]
Пример 2. Необходимо составить уравнения линейной регрессии и построить теоретические линии регрессии на основе исходных данных по длине листовой пластинки (х) и диаметру штамба (у), а также корреляционной решетки между этими признаками у 31 сеянца алычи:
Длина листовой пластинки «х», мм и диаметр штамба «у», см.
у 31 сеянца алычи
| х | 76,60 | 72,20 | 67,00 | 66,50 | 63,30 | 65,40 | 63,90 | 63,10 | 63,00 | 62,50 | 62,20 |
| у | 4,56 | 4,79 | 4,49 | 4,32 | 4,59 | 4,32 | 4,67 | 4,29 | 4,57 | 4,20 | 4,12 |
| х | 61,00 | 60,20 | 60,00 | 59,60 | 59,50 | 58,90 | 58,00 | 57,80 | 57,60 | 57,00 | |
| у | 4,13 | 4,70 | 3,80 | 4,23 | 3,76 | 4,08 | 4,61 | 4,37 | 4,30 | 4,00 | |
| х | 56,80 | 55,40 | 55,00 | 53,08 | 53,70 | 52,00 | 51,40 | 51,00 | 50,90 | 48,50 | |
| у | 3,82 | 4,12 | 4,19 | 4,16 | 4,09 | 4,12 | 4,02 | 4,31 | 4,06 | 4,03 |
Корреляционная решетка между длиной листовой пластинки «х» и диаметром штамба «у» у 31 сеянца алычи
| Границы классов | Классы по «х» | Сумма частот по «у» |
| ||||||||
| 47,0-51,4 | 51,5-55,9 | 56,0-60,4 | 60,5-64,9 | 65,0-69,4 | 69,5-73,9 | 74,0-78,4 | |||||
| Середины классов | 49,2 | 53,7 | 58,2 | 62,7 | 67,2 | 71,7 | 76,2 | ||||
| Классы по «у» | 4,66-4,80 | 4,73 | 1 | 1 | 1 | 3 | 64,20 | ||||
| 4,51-4,65 | 4,58 | 1 | 2 | 1 | 4 | 62,70 | |||||
| 4,36-4,50 | 4,43 | 1 | 1 | 2 | 62,70 | ||||||
| 4,21-4,35 | 4,28 | 1 | 2 | 1 | 2 | 6 | 60,45 | ||||
| 4,06-4,20 | 4,13 | 1 | 5 | 1 | 3 | 10 | 56,40 | ||||
| 3,91-4,05 | 3,98 | 1 | 1 | 1 | 3 | 53,70 | |||||
| 3,76-3,90 | 3,83 | 3 | 3 | 58,20 | |||||||
| Сумма частот по «х» | 3 | 6 | 10 | 7 | 3 | 1 | 1 | 31 | |||
|
| 4,13 | 4,11 | 4,19 | 4,37 | 4,33 | 4,73 | 4,58 |
| |||
Решение.
Существует два способа составления уравнений регрессии: 1) на основе корреляционной решетки; 2) на основе исходных данных. Второй способ дает более точные результаты поскольку оперирует со всей выборкой, а не с результатами разбивки, которая в той или иной степени проводится произвольно. Проведем вычисления по обоим способам.
а) Составление линейных уравнений регрессии на основе корреляционной решетки
1. Составим уравнение линейной регрессии у / х. Построим на основе корреляционной решетки таблицу для вычислений параметров первой системы уравнений:
Параметры для решения системы уравнений у / х
| середины классов по «x» |
| xy | x 2 |
| 49,2 | 4,13 | 203,20 | 2420,64 |
| 53,7 | 4,11 | 220,44 | 2883,69 |
| 58,2 | 4,19 | 243,86 | 3387,24 |
| 62,7 | 4,37 | 273,73 | 3931,29 |
| 67,2 | 4,33 | 290,98 | 4515,84 |
| 71,7 | 4,73 | 339,14 | 5140,89 |
| 76,2 | 4,58 | 349,00 | 5806,44 |
| Σ=438,90 | Σ=30,43 | Σ=1920,34 | Σ=28086,03 |
n (число классов)=7
1.1. Подставляем соответствующие значения в систему уравнений:
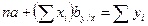
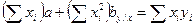
Система уравнений примет следующий вид:
1.2. Умножим все элементы первого уравнения на величину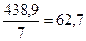 
, для того, чтобы уравнять значения коэффициентов перед параметром «а», второе уравнение оставим без изменений:
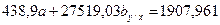
1.3. Вычтем из второго уравнения первое, получим следующее уравнение:
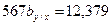
1.4. Вычисляем «by/x»:
by/x = 
1.5. Подставим значение «bу / х » в исходное первое уравнение:
тогда: 
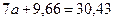
Отсюда следует, что:
а =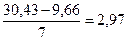 
1.6. Тогда уравнение регрессии у / х будет следующим:
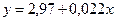
2. Для построения теоретической линии регрессии у/х определяем координаты переменной «у теор» по серединам классов переменной «х» исходя из уравнения регрессии у / х:
Координаты переменной «у теор» по серединам классов «х»
| середины классов по «х» | у теор | у эмп |
| 49,2 | 4,05 | 4,13 |
| 53,7 | 4,15 | 4,11 |
| 58,2 | 4,25 | 4,19 |
| 62,7 | 4,35 | 4,37 |
| 67,2 | 4,45 | 4,33 |
| 71,7 | 4,55 | 4,73 |
| 76,2 | 4,65 | 4,58 |
Как видно из табл. 6.6. значения теоретических и эмпирических значений переменной «у» очень близки друг другу.
2. Составляем уравнение линейной регрессии х / у. Для этого построим на основе корреляционной решетки таблицу для вычислений параметров второй системы уравнений:
Параметры для решения системы уравнений х / у
| середины классов по «y» |
| xy | y 2 |
| 3,83 | 53,70 | 205,67 | 14,67 |
| 3,98 | 56,40 | 224,47 | 15,84 |
| 4,13 | 58,20 | 240,37 | 17,06 |
| 4,28 | 60,45 | 258,73 | 18,32 |
| 4,43 | 62,70 | 277,76 | 19,62 |
| 4,58 | 62,70 | 287,17 | 20,98 |
| 4,73 | 64,20 | 303,67 | 22,37 |
| Σ=29,96 | Σ=418,35 | Σ=1797,83 | Σ=128,86 |
n (число классов=7
2.1. Подставляем соответствующие значения параметров в систему уравнений х / у:
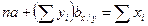
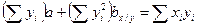
Система уравнений примет следующий вид:
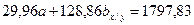
2.2. Умножаем первое уравнение на величину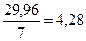 
для того, чтобы уравнять значения коэффициентов перед параметром «а»:
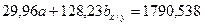
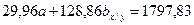
2.3. Вычитаем из второго уравнения первое, тогда:
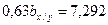
2.4. Вычисляем bx / y:
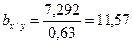
2.5. Подставим значение bх / у в исходное уравнение:
Тогда:
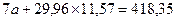
2.6. Уравнение регрессии х / у будет следующим:
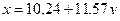
2.7. Для построения теоретической линии регрессии х / у определяем координаты переменной «x теор» по серединам классов переменной «y»:
Координаты переменной «х теор» по серединам классов «у»
| середины классов по «y» | x теор | x эмп |
| 3,83 | 54,55 | 53,70 |
| 3,98 | 56,29 | 56,40 |
| 4,13 | 58,02 | 58,20 |
| 4,28 | 59,76 | 60,45 |
| 4,43 | 61,50 | 62,70 |
| 4,58 | 63,23 | 62,70 |
| 4,73 | 64,97 | 64,20 |
Как видно из табл. 7.8. значения эмпирических и теоретических значений переменной «х» достаточно близки друг другу.
б) Составление линейных уравнений регрессии на основе исходных данных по х и у
1. Составим уравнение линейной регрессии у / х. Построим на основе исходных данных таблицу для вычислений параметров первой системы уравнений:
Параметры для решения системы уравнений у / х непосредственно из исходных данных
| х | у | ху | х 2 |
| 76,6 | 4,56 | 349,296 | 5867,56 |
| 72,2 | 4,79 | 345,838 | 5212,84 |
| 67,0 | 4,49 | 300,830 | 4489,00 |
| 66,5 | 4,32 | 287,280 | 4422,25 |
| 63,3 | 4,59 | 290,547 | 4006,89 |
| 65,4 | 4,32 | 282,528 | 4277,16 |
| 63,9 | 4,67 | 298,413 | 4083,21 |
| 63,1 | 4,29 | 270,699 | 3981,61 |
| 63,0 | 4,57 | 287,910 | 3969,00 |
| 62,5 | 4,20 | 262,500 | 3906,25 |
| 62,2 | 4,12 | 256,264 | 3868,84 |
| 61,0 | 4,13 | 251,930 | 3721,00 |
| 60,2 | 4,70 | 282,940 | 3624,04 |
| 60,0 | 3,80 | 228,000 | 3600,00 |
| 59,6 | 4,23 | 252,108 | 3552,16 |
| 59,5 | 3,76 | 223,720 | 3540,25 |
| 58,9 | 4,08 | 240,312 | 3469,21 |
| 58,0 | 4,61 | 267,380 | 3364,00 |
| 57,8 | 4,37 | 252,586 | 3340,84 |
| 57,6 | 4,30 | 247,680 | 3317,76 |
| 57,0 | 4,00 | 228,000 | 3249,00 |
| 56,8 | 3,82 | 216,976 | 3226,24 |
| 55,4 | 4,12 | 228,248 | 3069,16 |
| 55,0 | 4,19 | 230,450 | 3025,00 |
| 53,8 | 4,16 | 223,808 | 2894,44 |
| 53,7 | 4,09 | 219,633 | 2883,69 |
| 52,0 | 4,12 | 214,240 | 2704,00 |
| 51,4 | 4,02 | 206,628 | 2641,96 |
| 51,0 | 4,31 | 219,810 | 2601,00 |
| 50,9 | 4,06 | 206,654 | 2590,81 |
| 48,5 | 4,03 | 195,455 | 2352,25 |
| 1843,8 | 131,82 | 7868,663 | 110851,42 |
1.1. Подставляем соответствующие значения в систему уравнений:
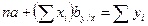
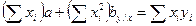
Система уравнений примет следующий вид:
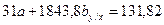
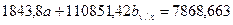
1.2. Умножим все элементы первого уравнения на величину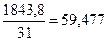 
, для того, чтобы уравнять значения коэффициентов перед параметром «а»:
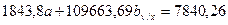
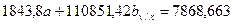
1.3. Вычтем из второго уравнения первое, получим следующее уравнение:
1.4. Вычисляем «by/x»:
by/x = 
1.5. Подставим значение «bу / х » в исходное первое уравнение:
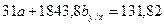
тогда: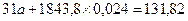 
Отсюда следует, что:
а = 
1.6. Тогда уравнение регрессии у / х будет следующим:
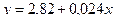
2. Для построения теоретической линии регрессии у / х определяем координаты переменной «у теор» по серединам классов переменной «х» исходя из уравнения регрессии у / х:
Координаты «у теор» по «х»
| х | у теор | у эмп |
| 48,5 | 3,98 | 4,03 |
| 50,9 | 4,04 | 4,06 |
| 51,0 | 4,04 | 4,31 |
| 51,4 | 4,05 | 4,02 |
| 52,0 | 4,07 | 4,12 |
| 53,7 | 4,11 | 4,09 |
| 53,8 | 4,11 | 4,16 |
| 55,0 | 4,14 | 4,19 |
| 55,4 | 4,15 | 4,12 |
| 56,8 | 4,18 | 3,82 |
| 57,0 | 4,19 | 4,00 |
| 57,6 | 4,20 | 4,30 |
| 57,8 | 4,21 | 4,37 |
| 58,0 | 4,21 | 4,61 |
| 58,9 | 4,23 | 4,08 |
| 59,5 | 4,25 | 3,76 |
| 59,6 | 4,25 | 4,23 |
| 60,0 | 4,26 | 3,80 |
| 60,2 | 4,26 | 4,70 |
| 61,0 | 4,28 | 4,13 |
| 62,2 | 4,31 | 4,12 |
| 62,5 | 4,32 | 4,20 |
| 63,0 | 4,33 | 4,57 |
| 63,1 | 4,33 | 4,29 |
| 63,3 | 4,34 | 4,59 |
| 63,9 | 4,35 | 4,67 |
| 65,4 | 4,39 | 4,32 |
| 66,5 | 4,42 | 4,32 |
| 67,0 | 4,43 | 4,49 |
| 72,2 | 4,55 | 4,79 |
| 76,6 | 4,66 | 4,56 |
Как видно из табл. 90 значения теоретических и эмпирических значений переменной «у» достаточно близки друг другу.
2. Составляем уравнение линейной регрессии х / у. Для этого построим на основе исходных данных таблицу для вычислений параметров второй системы уравнений:
Параметры для решения системы уравнений х / у непосредственно из исходных данных
| у | х | ху | у 2 |
| 4,56 | 76,6 | 349,296 | 20,7936 |
| 4,79 | 72,2 | 345,838 | 22,9441 |
| 4,49 | 67,0 | 300,830 | 20,1601 |
| 4,32 | 66,5 | 287,280 | 18,6624 |
| 4,59 | 63,3 | 290,547 | 21,0681 |
| 4,32 | 65,4 | 282,528 | 18,6624 |
| 4,67 | 63,9 | 298,413 | 21,8089 |
| 4,29 | 63,1 | 270,699 | 18,4041 |
| 4,57 | 63,0 | 287,910 | 20,8849 |
| 4,20 | 62,5 | 262,500 | 17,6400 |
| 4,12 | 62,2 | 256,264 | 16,9744 |
| 4,13 | 61,0 | 251,930 | 17,0569 |
| 4,70 | 60,2 | 282,940 | 22,0900 |
| 3,80 | 60,0 | 228,000 | 14,4400 |
| 4,23 | 59,6 | 252,108 | 17,8929 |
| 3,76 | 59,5 | 223,720 | 14,1376 |
| 4,08 | 58,9 | 240,312 | 16,6464 |
| 4,61 | 58,0 | 267,380 | 21,2521 |
| 4,37 | 57,8 | 252,586 | 19,0969 |
| 4,30 | 57,6 | 247,680 | 18,4900 |
| 4,00 | 57,0 | 228,000 | 16,0000 |
| 3,82 | 56,8 | 216,976 | 14,5924 |
| 4,12 | 55,4 | 228,248 | 16,9744 |
| 4,19 | 55,0 | 230,450 | 17,5561 |
| 4,16 | 53,8 | 223,808 | 17,3056 |
| 4,09 | 53,7 | 219,633 | 16,7281 |
| 4,12 | 52,0 | 214,240 | 16,9744 |
| 4,02 | 51,4 | 206,628 | 16,1604 |
| 4,31 | 51,0 | 219,810 | 18,5761 |
| 4,06 | 50,9 | 206,654 | 16,4836 |
| 4,03 | 48,5 | 195,455 | 16,2409 |
| 131,82 | 1843,8 | 7868,663 | 562,6978 |
2.1. Подставляем соответствующие значения параметров в систему уравнений х / у:
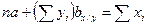
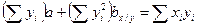
Система уравнений примет следующий вид:
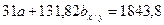
2.2. Умножаем первое уравнение на величину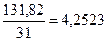 
для того, чтобы уравнять значения коэффициентов перед параметром «а»:
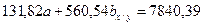
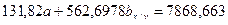
2.3. Вычитаем из второго уравнения первое, тогда:
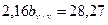
2.4. Вычисляем bx / y:
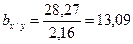
2.5. Подставим значение bх / у в исходное уравнение:
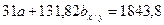
Тогда:
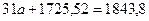
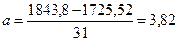
2.6. Уравнение регрессии х / у будет следующим:
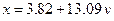
2.7. Для построения теоретической линии регрессии х / у определяем координаты «x теор» по «y»:
Координаты «х теор» по «у»
| у | хтеор | х |
| 3,76 | 53,04 | 59,5 |
| 3,80 | 53,56 | 60,0 |
| 3,82 | 53,82 | 56,8 |
| 4,00 | 56,18 | 57,0 |
| 4,02 | 56,44 | 51,4 |
| 4,03 | 56,57 | 48,5 |
| 4,06 | 56,97 | 50,9 |
| 4,08 | 57,23 | 58,9 |
| 4,09 | 57,36 | 53,7 |
| 4,12 | 57,75 | 62,2 |
| 4,12 | 57,75 | 55,4 |
| 4,12 | 57,75 | 52,0 |
| 4,13 | 57,88 | 61,0 |
| 4,16 | 58,27 | 53,8 |
| 4,19 | 58,67 | 55,0 |
| 4,20 | 58,80 | 62,5 |
| 4,23 | 59,19 | 59,6 |
| 4,29 | 59,98 | 63,1 |
| 4,30 | 60,11 | 57,6 |
| 4,31 | 60,24 | 51,0 |
| 4,32 | 60,37 | 66,5 |
| 4,32 | 60,37 | 65,4 |
| 4,37 | 61,02 | 57,8 |
| 4,49 | 62,59 | 67,0 |
| 4,56 | 63,51 | 76,6 |
| 4,57 | 63,64 | 63,0 |
| 4,59 | 63,90 | 63,3 |
| 4,61 | 64,16 | 58,0 |
| 4,67 | 64,95 | 63,9 |
| 4,70 | 65,34 | 60,2 |
| 4,79 | 66,52 | 72,2 |
Как видно из табл. 6.12 значения эмпирических и теоретических значений переменной «х» достаточно близки друг другу.
3. Используя мастер диаграмм программы Excel строим две теоретические линии регрессии «у / х»и«х / у» (на основе уравнений линейной регрессии, полученных способом анализа исходных данных):
Рис. 6.4. Теоретические линии регрессии у / х (голубая) и х / у (красная
Вычисление коэффициентов регрессии [ 10 мин. ]
Пример 3. На основе данных примера 1 вычислите коэффициенты регрессии
Решение:
1. 
2. 
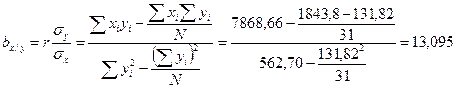
Практическое задание 7.1. У 20 плодов яблони сорта «Айдаред» были измерены масса плода «х» (г) и диаметр плода «у» (мм). Постройте корреляционную решетку. Постройте эмпирические и теоретические линии регрессии и вычислите коэффициенты регрессии by/x и bx/y.
| х | 165 | 176 | 175 | 168 | 167 | 172 | 175 | 180 | 179 | 173 |
| y | 56 | 75 | 70 | 61 | 61 | 63 | 72 | 80 | 76 | 68 |
| x | 166 | 178 | 169 | 169 | 170 | 176 | 180 | 169 | 177 | 176 |
| y | 58 | 76 | 60 | 64 | 63 | 71 | 78 | 63 | 75 | 71 |
Решение:
