Первое понятие вводят для геометрического представления движения материальных точек.
Траектория – это воображаемая линия в пространстве, множество точек которой определяет положение м. т. в различные моменты времени (по которой со временем перемещается м.т.)
Движение м.т. задано, если известно ее положение в каждый момент времени, то есть известен закон движения.
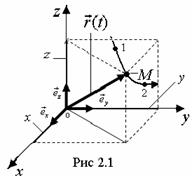
Радиус - вектор точки – направленный отрезок прямой, проведенный из начала координат в точку (рис 2.1). Если положения м.т. изменяется со временем, то
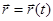 , (2.1)
, (2.1)
- радиус-вектор оказывается векторной функцией скалярного аргумента t (времени). С течением времени конец вектора 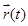 будет описывать траекторию точки. Для задания
будет описывать траекторию точки. Для задания 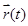 , в соответствии с определением, необходимо только наличие тела отсчета – вид системы координат не имеет значения. Движение задается в бескоординатной, т.е. векторной форме, т.к.
, в соответствии с определением, необходимо только наличие тела отсчета – вид системы координат не имеет значения. Движение задается в бескоординатной, т.е. векторной форме, т.к. 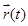 определяет положение м.т. в каждый момент t.
определяет положение м.т. в каждый момент t.
Проекции вектора в декартовой системе координат.
 Пусть некоторая точка О принята за начало отсчета.
Пусть некоторая точка О принята за начало отсчета.
 Возьмем (прямоугольную) декартову систему координат, начало которой совпадает с точкой О. Положение любой точки можно охарактеризовать либо ее радиус-вектором
Возьмем (прямоугольную) декартову систему координат, начало которой совпадает с точкой О. Положение любой точки можно охарактеризовать либо ее радиус-вектором 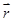 , либо тремя числами (x, y, z), являющимися декартовыми координатами этой точки. Установим связь между
, либо тремя числами (x, y, z), являющимися декартовыми координатами этой точки. Установим связь между  и числами x, y, z. Для этого полезно ввести единичные безразмерные векторы, направленные в положительном направлении осей X, Y, Z и обозначаемые, соответственно, как
и числами x, y, z. Для этого полезно ввести единичные безразмерные векторы, направленные в положительном направлении осей X, Y, Z и обозначаемые, соответственно, как 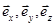 , которые называют ортами. Принимая во внимание правило сложения векторов, можно представить радиус-вектор в виде суммы трех векторов
, которые называют ортами. Принимая во внимание правило сложения векторов, можно представить радиус-вектор в виде суммы трех векторов 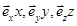 также направленных вдоль осей координат:
также направленных вдоль осей координат:

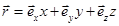
Числа x, y, z называют проекциями радиус-вектора 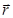 . Они совпадают с координатами точки, которую характеризует
. Они совпадают с координатами точки, которую характеризует 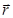 .
.
Не только радиус-вектор, но и любой другой вектор может быть представлен в виде суммы векторов, направленных вдоль осей координат (рис. 2.2):
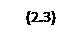
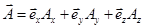
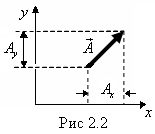
 Если
Если 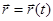 ,то, очевидно, x, y, z будут функциями t и определяет положение точки на траектории в каждый момент времени. Задание x(t), y(t), z(t) определяет координатную форму описания движения. В зависимости от характера движения эта форма может использовать различные системы координат. Примеры:
,то, очевидно, x, y, z будут функциями t и определяет положение точки на траектории в каждый момент времени. Задание x(t), y(t), z(t) определяет координатную форму описания движения. В зависимости от характера движения эта форма может использовать различные системы координат. Примеры:
1. М.т. движется равномерно из начала координат вдоль оси х. Уравнения, описывающие движение (траекторию) имеют вид х=At, y=0, z=0
2. М.т. равномерно вращается вокруг оси Z по окружности радиуса R. Используем цилиндрическую систему координат, полагая, что в момент t=0; 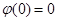 Тогда движение м.т. будет описываться формулами
Тогда движение м.т. будет описываться формулами 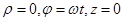 (ω-константа).
(ω-константа).
Если траектория задана, то задача сводится к указанию закона движения вдоль нее. Некоторая точка траектории принимается за начальную (рис 2.1), а любая другая точка характеризуется расстоянием s вдоль нее от начальной точки. В этом случае движение описывается формулой
 s = s(t),
s = s(t),
которая определяет путь, пройденный точкой за время t. Например, закон равномерного движения по окружности будет иметь вид s=At, где для рассмотренного выше примера A=ωR.
Вектор перемещения - это изменение (приращение) радиус-вектора за время Δt
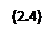
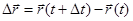
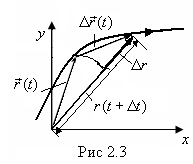
 Значение вектора (перемещения) равно расстоянию между точками траектории, в которой находится объект в момент
Значение вектора (перемещения) равно расстоянию между точками траектории, в которой находится объект в момент 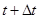 и t. Следует иметь ввиду, что в общем случае модуль
и t. Следует иметь ввиду, что в общем случае модуль 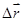 ,
, 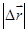 не равен приращению модуля
не равен приращению модуля 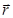 ,
, 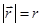 , равного
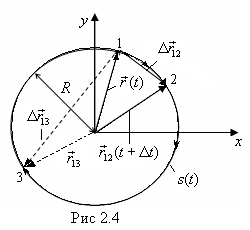
, равного 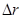 . Это имеет место даже при прямолинейном движении, если начало координат не совпадает с одной из точек траектории (рис 2.3). Другой пример, м.т. вращается по окружности радиуса R. Начало координат расположено в центре окружности (рис2.4).
. Это имеет место даже при прямолинейном движении, если начало координат не совпадает с одной из точек траектории (рис 2.3). Другой пример, м.т. вращается по окружности радиуса R. Начало координат расположено в центре окружности (рис2.4). 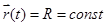 ;
;  ;
; 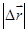 равен хорде.
равен хорде.
Скорость.
Вектор перемещения однозначно определяет в каждый момент t+Δt положение точки в пространстве.
Поэтому можно записать
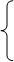
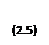
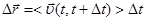
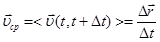
или
 Векторный коэффициент пропорциональности между вектором приращения и промежутком времени Δt, за который произошло это приращение называют средней скоростью (
Векторный коэффициент пропорциональности между вектором приращения и промежутком времени Δt, за который произошло это приращение называют средней скоростью ( ). Угловыми скобками мы в дальнейшем будем обозначать любые средние значения физических величин при изменении соответствующей независимой переменной. В круглых скобках <
). Угловыми скобками мы в дальнейшем будем обозначать любые средние значения физических величин при изменении соответствующей независимой переменной. В круглых скобках < 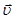 > указан промежуток Δt, для которого вычислена средняя скорость и начало его отсчета t.
> указан промежуток Δt, для которого вычислена средняя скорость и начало его отсчета t.
При неограниченном уменьшении Δt средняя скорость стремится к предельному значению, которое называют мгновенной скоростью, или, просто скоростью.
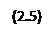
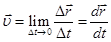
Таким образом, скорость 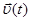 в каждый момент времени t определяется отношением бесконечно малого (элементарного) вектора перемещения
в каждый момент времени t определяется отношением бесконечно малого (элементарного) вектора перемещения 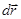 к бесконечно малому интервалу времени dt, за который происходит такое изменение радиуса-вектора. Приращение радиус-вектора
к бесконечно малому интервалу времени dt, за который происходит такое изменение радиуса-вектора. Приращение радиус-вектора 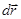 есть приращение относительно системы, орты которой жестко скреплены с телом отсчета. В связи с этим скорость точки
есть приращение относительно системы, орты которой жестко скреплены с телом отсчета. В связи с этим скорость точки 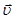 относительно системы отсчета следует рассматривать как производную радиус-вектора по времени. При постоянных ортах
относительно системы отсчета следует рассматривать как производную радиус-вектора по времени. При постоянных ортах 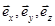 проекции которой на оси системы координат Декарта равны:
проекции которой на оси системы координат Декарта равны:
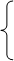

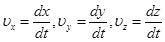
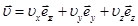
Если предположить, что параметры траектории известны, то в качестве аргумента радиуса-вектора можно взять путь s = s(t). Траектория будет задана уравнением 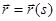 , а радиус-вектор станет сложной функцией t:
, а радиус-вектор станет сложной функцией t:
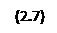
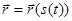
Использовав правило дифференцирования сложной функции, из (2.7) находим:
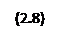
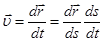

Но величина Δs – расстояние между двумя точками траектории, а 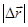 -кратчайшее расстояние (по прямой). Ясно (рис 2.5) при Δt→0
-кратчайшее расстояние (по прямой). Ясно (рис 2.5) при Δt→0 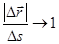 . Вводя единичный вектор
. Вводя единичный вектор 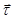 , направленный вдоль касательной к траектории в момент t, следовательно, можно записать:
, направленный вдоль касательной к траектории в момент t, следовательно, можно записать:
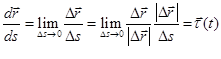 (2.9)
(2.9)
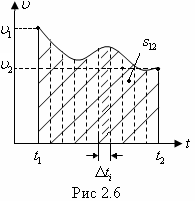 Т.к.
Т.к. 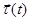 - единичный вектор, то с течением времени (на разных участках траектории) он может изменять только направление. Кроме того,
- единичный вектор, то с течением времени (на разных участках траектории) он может изменять только направление. Кроме того, 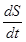 оказывается модулем скорости
оказывается модулем скорости 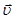 , и формула (2.8) приобретает вид:
, и формула (2.8) приобретает вид:


- скорость всегда направлена по касательной к траектории.
Зная зависимость 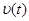 , нетрудно получить формулу для определения пути, проходимого м.т. за промежуток времени t2 – t1=Δ t12. Для этого разобьем промежуток на N малых интервалов Δti: Δt1, Δt2,…ΔtN (Рис.2.6)
, нетрудно получить формулу для определения пути, проходимого м.т. за промежуток времени t2 – t1=Δ t12. Для этого разобьем промежуток на N малых интервалов Δti: Δt1, Δt2,…ΔtN (Рис.2.6)
Весь путь s12 точки будет равен:
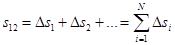
Т.к. интервалы Δti малы (→0), то в пределах каждого 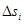 можно считать
можно считать 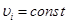 ,и
,и 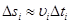 . При стремлении каждого промежутка Δti к нулю точность этого выражения будет возрастать, при одновременном увеличении числа промежутков. Поэтому точное значение будет описываться формулой:
. При стремлении каждого промежутка Δti к нулю точность этого выражения будет возрастать, при одновременном увеличении числа промежутков. Поэтому точное значение будет описываться формулой:
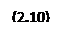
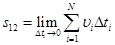
Ее записывают в виде:
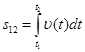 (2.11)
(2.11)
и называют определенным интегралом от функции 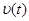 , взятого в пределах от t1 доt2. Из рис 2.6 видно, что
, взятого в пределах от t1 доt2. Из рис 2.6 видно, что  равна площади, заключенной между
равна площади, заключенной между 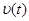 и осью t на участке Δ t12 . Заметим, что среднее значение модуля скорости в интервале
и осью t на участке Δ t12 . Заметим, что среднее значение модуля скорости в интервале 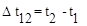 равно:
равно:
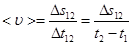 (2.12)
(2.12)
Иногда эту скалярную величину называют средней путевой скоростью. Используя (2.11), находим:
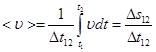 (2.13)
(2.13)
Очевидно, аналогично должны вычисляться и средние значения любых других скалярных или векторных функций. Например,

т.е.
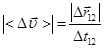 (2.14)
(2.14)
Вместо пройденного пути модуль средней скорости определяется длиной вектора перемещения.
Ускорение.
Ускорением называют “скорость” изменения скорости. Среднее ускорение следует из соотношения, аналогичного (2.5):
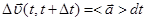
или
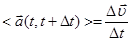 (2.15)
(2.15)
Соответственно, ускорение равно:
 (2.16)
(2.16)
- т.е. это производная от скорости по времени. При известной зависимости  ускорение можно найти, вычислив вторую производную от
ускорение можно найти, вычислив вторую производную от 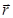 по времени. Чтобы проанализировать, как изменяет ускорение вектор скорости воспользуемся формулой (2.10). В общем случае при криволинейном движении изменяется не только модуль скорости
по времени. Чтобы проанализировать, как изменяет ускорение вектор скорости воспользуемся формулой (2.10). В общем случае при криволинейном движении изменяется не только модуль скорости 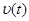 , но и направление (рис 2.5), т.е.
, но и направление (рис 2.5), т.е. 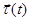 в процессе перемещения точки поворачивается. Поэтому
в процессе перемещения точки поворачивается. Поэтому
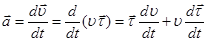 (2.17)
(2.17)
Для описания сложных кривых в аналитической геометрии в каждой точке кривой вводят три ортогональных орта, которые называют сопровождающим (или естественным) трехгранником - 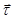 ,
, 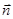 - орт перпендикулярный
- орт перпендикулярный 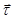 и лежащий в плоскости, где расположен элемент ds (
и лежащий в плоскости, где расположен элемент ds (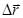 и
и 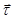 ), и орт
), и орт 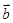 , перпендикулярный этой плоскости (рис 2.5). Элементарное приращение любого вектора, постоянной длины, перпендикулярно самому вектору. Например, используя условие
, перпендикулярный этой плоскости (рис 2.5). Элементарное приращение любого вектора, постоянной длины, перпендикулярно самому вектору. Например, используя условие 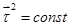 и дифференцируя обе части равенства, получаем
и дифференцируя обе части равенства, получаем 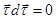 , что и доказывает утверждение. Воспользовавшись (2.9) для
, что и доказывает утверждение. Воспользовавшись (2.9) для 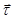 ,
, 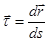 и учитывая, что
и учитывая, что 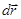 и
и 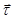 лежат в одной плоскости, находим:
лежат в одной плоскости, находим:
 ,
, 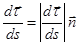 ,
, 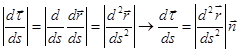 (2.18)
(2.18)
Величина 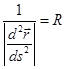 равна, так называемому, радиусу кривизны траектории. Радиус кривизны определяется как отношение элементарного приращения длины дуги ds к
равна, так называемому, радиусу кривизны траектории. Радиус кривизны определяется как отношение элементарного приращения длины дуги ds к  - углу между
- углу между 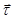 и
и 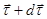 (см. рис 2.5)
(см. рис 2.5)

или
 (2.19)
(2.19)
Можно сказать, что R – это радиус окружности, элемент дуги которой совпадает с рассматриваемым малым участком траектории (кривой). Центр такой окружности называют центром кривизны для данного элемента ds. Из рис 2.5 видно, что т.к.  , то
, то 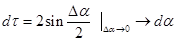
Поэтому из (2.19) следует:
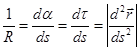 (2.20)
(2.20)
Т.к. 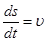 ,то подставляя (2.18) (2.20) в (2.17), окончательно получим:
,то подставляя (2.18) (2.20) в (2.17), окончательно получим:
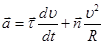 (2.21)
(2.21)
Полное ускорение состоит из двух взаимно перпендикулярных векторов: ускорения 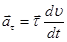 , направленного вдоль траектории движения, которое называют тангенциальным, и ускорения
, направленного вдоль траектории движения, которое называют тангенциальным, и ускорения  , направленного перпендикулярно траектории по главной нормали, т.е. к центу кривизны траектории, и называемого нормальным. Компонента
, направленного перпендикулярно траектории по главной нормали, т.е. к центу кривизны траектории, и называемого нормальным. Компонента 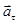 определяет изменение модуля скорости
определяет изменение модуля скорости  . Т.к. нормальное ускорение
. Т.к. нормальное ускорение 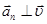 , то оно лишь поворачивает вектор скорости, “искривляет” траекторию, оставляя абсолютное значение
, то оно лишь поворачивает вектор скорости, “искривляет” траекторию, оставляя абсолютное значение 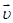 неизменным.
неизменным.
При движении точки по окружности нормальное ускорение называют центростремительным, поскольку центр кривизны траектории для всех ее точек один и тот же и совпадает с центром окружности. Т.к. 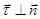 , то формула для модуля полного ускорения имеет вид:
, то формула для модуля полного ускорения имеет вид:
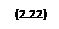
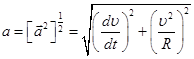

 2020-10-11
2020-10-11 987
987







