2020-10-12
97
Поле объемно заряженного шара
Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r (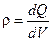
- заряд, приходящийся на единицу объема). Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что ив случае сферической поверхности:
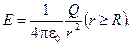
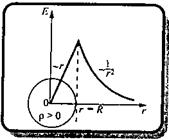
Внутри шара напряженность другая. Сфера радиуса r' < R охватывает заряд Q'=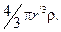 
Поэтому, согласно теореме Гаусса, 4pr'2E = Q'/e0= 
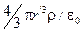, Учитывая, что 
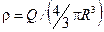, получим
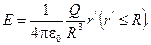
График зависимости Е от г приведен на рисунке.
Поле равномерно заряженного бесконечного цилиндра (нити)
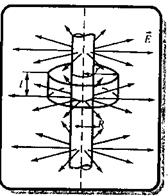Бесконечный цилиндр радиуса R заряжен равномерно с линейной плотностью t (
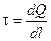- заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой /. Поток вектора 
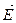сквозь торцы цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность -2prlЕ. По теореме Гаусса, при r > R 2prlE= t//e0, откуда
|
|
|
.
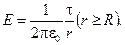Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0.
|
|
Циркуляция вектора напряженности электростатического поля
