Принцип суперпозиции (наложения) электростатических полей
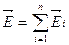 Напряженность
Напряженность 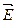 результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
Электрический диполь
Система двух равных по модулю разноименных точечных зарядов (+Q, -Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля.
Плечо диполя
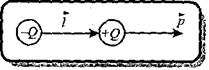 Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними.
Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними.
Электрический момент диполя
Вектор  совпадающий по направлению с плечом диполя.
совпадающий по направлению с плечом диполя.
По принципу суперпозиции, напряженность поля диполя в произвольной точке 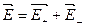 (
( — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами).
— напряженности полей, создаваемых соответственно положительным и отрицательным зарядами).
Напряженность поля
На продолжении оси диполя
В точке А
 |

l/2<<r, поэтому  .
.
Теорема Гаусса для
Электростатического поля в вакууме
Поток вектора 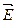 сквозь сферическую поверхность радиуса r
сквозь сферическую поверхность радиуса r
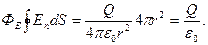
Этот результат справедлив* для замкнутой
поверхности любой формы. Так, если
окружить сферу (см. рисунок) произвола
ной замкнутой поверхностью, то каждая
линия напряженности, пронизывающая
сферу, пройдет и сквозь эту поверхность.
Общий случай: произвольная поверхность, окружающая n зарядов
В соответствии с принципом суперпозиции напряженность 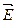 поля, создаваемого всеми зарядами, равна сумме напряженностей
поля, создаваемого всеми зарядами, равна сумме напряженностей 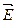 , создаваемых каждым зарядом в отдельности:
, создаваемых каждым зарядом в отдельности: 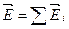 . Поэтому
. Поэтому
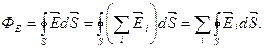
Каждый из интегралов, стоящий под знаком суммы, равен 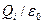 . Следовательно,
. Следовательно, 
Теорема Гаусса для поля в вакууме
Лоток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленных на ε0: 
Если заряд распределен в пространстве с объемной плотностью 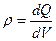 , то теорема Гаусса для электростатического поля в вакууме
, то теорема Гаусса для электростатического поля в вакууме
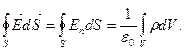
 2020-10-12
2020-10-12 126
126







