2020-10-12
117
Если перемещать заряд Qo из произвольной точки за пределы поля, т. е. в бесконечность, где по условию потенциал равен нулю, то работа сил электростатического поля, согласно формуле (1),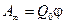 
, откуда
Потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки в бесконечность.
Принцип суперпозиции (наложения) электростатических полей
Если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов.
 |
Напряженность как градиент потенциала
Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и х2 - х{ = dх, равна Ехdх. Та же работа равна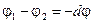 
. Приравняв оба выражения, получим
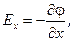
где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей y и z, имеем
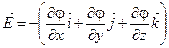, или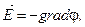 
(
— единичные векторы координатных осей х, у, z). Знак минус показывает, что вектор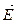 
направлен в сторону убывания потенциала.
Поле равномерно заряженной бесконечной
плоскости
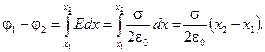Е = s/(2e0)). Разность потенциалов между точками, лежащими на расстояниях x1 и х2 от плоскости, равна
Поле равномерно заряженной сферической
поверхности
Радиус сферы R, общий заряд Q. При r > R (см. с. 100). Разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра сферы (r] >R, r2>R), равна
 |
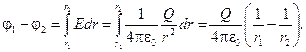(1)
Если принять r, = r и r2 = ¥, то потенциал поля вне сферической поверхности задается выражением j = Q/(4pe0r).
