Синусоидалы ток тізбегіндегі индуктивтілік 10 страница

Т уақытының аралық шегінде бірінші жақтың үзілу саны, сонымен қатар f(t) функциясының максимумдары мен минимумдарының саны шекті деп есептейік. Осылайша, Дирихле шартын қанағаттандыратын функцияларды қарастырамыз; шынайы электр тізбегіндегі ЭҚК, тоқ және кернеу осы шарттарды қанағаттандыратындығын аңғарған жөн.

Дирихле шарттарын қанағаттандыратын периодты синусоидалы емес функция шексіз гармоникалық қатар Фурье қатары түрінде келуі мүмкін. Бұл қатардың қосындысы бұл функцияның барлық үздіксіздіктеріне арналған  мәндерімен сәйкес келеді, ал үзілку нүктесінде  шекті мәннің оң және солының орташа арифметикалығын береді, яғни

 

.

 

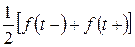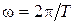 етіп белгілеп, w негізгі бұрыштық жиілік деп атаймыз.  w бұрыштық жиілікті синусоидалы және косинусоидалы қосындылауыштар негізгі гармониканы түзеді. Аса жоғары бұрыштық жиілікті қосындылауыш жоғарғы гармониканы білдіреді.                                                  Гармоникалық қатар тригонометриялық түрде келесі формула бойынша есептелінеді

 

                 ,                     (8.1)

 

мұндағы

 

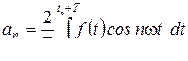                     ;                                    (8.2)

 

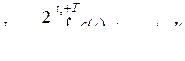                         ;                                     (8.3)

 

мұндағы 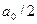 – тұрақты қосындылауыш;

                   а_n және b_n – қатардың косинусоидалы және синусоидалы мүшелерінің амплитудалары.

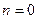 кезінде 8.2 мәнінің негізінде анықталатын  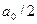тұрақты қосындылауыш  функциясының мерзім үшін орташа мәнін білдіреді. 8.2 суретте бейнеленген оң және теріс мәндердің ауданы  бірдей болғанда, ол нөле тең болады.

 

 

 

8.2 Сурет – Мерзім үшін орташа мәні нөлге тең синусоидалы емес функция

 

Фурье қатарының а_n және b_n коэффициенттері 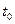-ге тәуелді емес; сондықтан  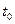мәні еркін таңдалынуы мүмкін. (8.2) және (8.3) формулаларындағы интеграласты функция Т периодына ие екендігін есепке алсақ, оған оңай көз жеткізуге болады. Интеграласты функциясын  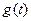арқылы белгілегенде алатынымыз

 

 

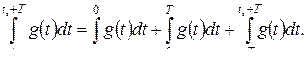
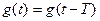 болатындықтан,

 

 

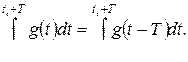
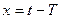айнымалысын алмастыру арқылы табатынымыз

 

.

 

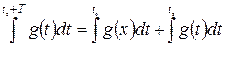Кезегінше,

 

 

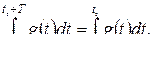
Алынған нәтижені былай да түсіндіруге болады: және 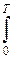 интегралдары білдіретін аудандар тең, себебі интеграласты функциясының мерзімдік күшіне орай t 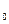-дің кез-келген өзгерісі берілген функция мен мерзім үшін абциссалар осі шектейтін ауданды өзгертпейді.  

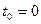 етіп қойып,  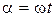жаңа айнымалысын енгізе отырып ( 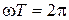 және 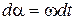 екенін есепке ала отырып), келесі формуланы анықтаймыз

 

                        ,                 (8.4)

мұндағы

 

                                 ;                             (8.5)

 

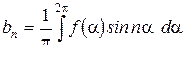                              .                             (8.6)

 

 етіп қабылдасақ, онда интеграциялану шегі сәйкесінш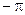е  және 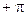-ге тең болады.

 (8.1) немесе (8.4) формулалары білдіретін косинусоида мен синусоида қосындысы, тек сәйкес бастапқы фазалары бар бір синусоидалардың қосындысы түрінде келуі мүмкін.

Егер шартты қабылдасақ

 

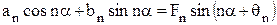                             ,              (8.7)

 

мұндағы

 

 

 

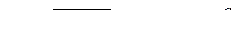
онда қатар келесі түрге ие болады

 

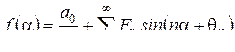                              .                    (8.8)

 

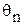 бұрышы (синус пен косинус белгісін анықтайтын) а_n және b_n  белгілерін есепке алатынынеске салайық.

(8.8) формасы әрбір гармониканың пайыздық арақатынасын білу қажет жағдайда ғана ыңғайлы; ол әдетте электр тізбектеріндегі синусоидалы емес тоқ пен кернеуді есептеу үшін қолданылады  (8.5 параграфты қара).

Фурье теориялық қатарында қосындылауыштың шексіз саны болса да, ол тез шығарылады. Шығарылған қатар берілген функцияны кез-келген талап етілген нақтылық дәрежесінде бейнелеуі мүмкін; егер ол ез шығарылса, онда талап етілетін нақтылық дәрежесін алу үшін гармониканың шағын мөлшерін алсақ та жетеді.

Тәжірибиеде кездесетін мерзімді синусоидалы емес функциялар екі топқа бөлінуі мүмкін. Бірінші топқа геометриялық дұрыс формалы қисықтар, ал екінші топқа күрделі формалы қисықтар жатқызылады; оларда Фурье қатарына жіктеу графоаналитикалық түрде жүргізіледі.

Фурье қатарына графоаналиикалық әдісі сандық интеграциялаудың жақындатылған әдісін білдіреді. Ол кезде белгілі интегралды есептеу қосындылауыштардың шекті санының қосындысын табумен алмастырылады. Осы мақсатта 2 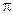-ге тең  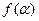функциясының мерзімі 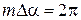болатындай етіліп, 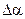-ның  m тең аралығына бөлінеді.

Координаталардың басынан k аралығына дейінгі қашықтық 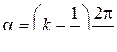 бұрышын құрайды.

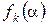   k аралығы ортасындағы мерзімді синусоидалы емес функциясының мәне бола берсін. 

(8.5) және (8.6) мәндеріне енетін интегралдар мына қосындылармен алмастырылады

 

 

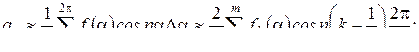
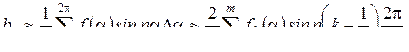
Егер мерзім шегінде үзілу нүктелері болса, онда берілген жіктеудің графикалық әдісі кезінде аралықтарға бөлуді үзілу нүктелері аралықтың орталарында болмайтындай етіп жасаған жөн болар.

Жоғарыда сипатталған Фурье қатарына графоаналитикалық жіктеуді орындау техникасы кезінде функция мәндері аралықтың ортасында алынған; егер оның орнына мәндерді аралықтың басында немесе соңында алсақ, онда жұп функцияда жоқ синусоидалар да пайда болады.

 

8.2 Симметрия жағдайы

Электрлік және магнит шамаларын бейнелейтін мерзімдік сиеусоидалы емес функцияларында симметрияның қандай да бір түрі болады және ол Фурье қатарына жіктеуді оңайлатады.

Симметрияның келесі жағдайларын қарастырайық:

8.2.1 Функциясы ординаттар осіне қатысты симметриялы яғни 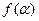= 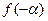, ол 8.3 суретінде бейнеленген. Бұндай функциялар жұп дпе аталады. Кез-келген жиіліктің синусоидалары тақ функция болатындықтан, олар қатар құрамына енбейді.

 

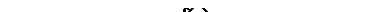
8.3 Сурет –  Ординаттар осіне қатысты симметриялы функция

 

Сондықтан симметрияның берілген түрі кезінде

 

,

 

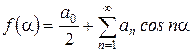яғни, жұп функцияда 8.3 суретінде көрсетілгендей, тек косинусоида мен тұрақты құрауыш қана болады.

        

 

Жұп функцияның тағы бір маңызды қасиеті а_n коэфиценттерін анықтау үшін жарты мерзім бойында f () қисығын ғана пайдалану жеткілікті болатындығында, яғни

 

                                      .                        (8.9)

 

Бұл келесі теңдіктен шығады

 

 

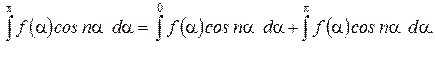
Бірінші аралықта -ны 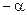-ға алмастыру  (8.9) формуласына әкеледі.

8.2.2 8.4 суретіне сәйкес 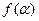 функциясы координаттар басына қатысты симметриялы, яғни = ().

 

 

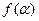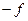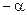8.4 Сурет – Координаттар басына қатысты симметриялы функция

          

      Бұндай функциялар тақ деп аталады. Тұрақты қосындылауыш пен косинусоида бұл жағдайды қанағаттандырмайтындықтан, симметрияның берілген түрінде қатар келесі түрге ие болады

 

 

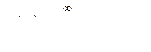
яғни тақ функцияда тек синусоидалы ғана болуы мүмкін.

Бұнда да алдыңғы жағдайдағы сияқты  b_n  коэфиценттерін анықтау үшін жарты мерзім бойында тек 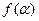 қисығын пайдаланса ғана болғаны, яғни

 

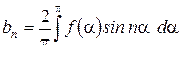                                      .                   (8.10)

 

8.2.3  8.5 суретіне сәйкес f() функциясы екі жартылай мерзімді уақыт бойынша қатарластырған кезде абциссалар осіне қатысты симметриялы, яғни  = .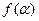

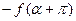(8.4) формуласына сәйкес 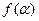-ны алмастыра отырып, алатынымыз 

 

 

бұдан n жұбы үшін

 

 

 

8.5 Сурет – Абциссалар осіне қатысты симметриялы функция

 

Бұл жағдайда жұп n кезінде а_n=0 және а_n= b_n= 0 болса, α (альфа) еркін мәндері кезінде қанағаттандырылады.

Сондықтан симметрияның берілген түрінде  

 

 

яғни уақыт бойынша екі жартылай мерзімді қатарластырған кездегі абциссалар осіне қатысты симметриялы функцияда тек тақ гармоникалар ғана болады.

Бұл жағдайда а_n және b_n коэффиценттері (8.9) және (8.10) формулалары бойынша есептелінуі мүмкін.

Мерзімді синусоидалы емес функцияны Фурье қатарына орналастырғанда, алдын-ала берілген функция симметрияның қандай да бір түріне ие емес пе екендігін анықтап алған жөн. Симметрияның болуы жіктеу барысында қандай гармоникаларды күтуге болатындығын болжауға мүмкіндік береді.

Егер симметрия шарттары біруақытта 1 және 3 пп. бойынша орындалса, онда жіктеуде тек тақ косинусоидалар, егер 2 және 3 пп. бойынша орындалса, онда тек тақ синусоидалар болады.

Енді тек тақ косинусоидалары ғана бар функция, сонымен қатар

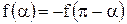 шартын да қанағаттандырады делік. Тақ кезінде  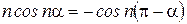болатындықтан, бұл жағдайда  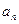коэффиценттерін анықтау үшін периодтың төрттен бір бөлігі бойында  f (α) қисығын пайдалану жеткілікті

 

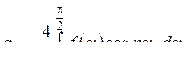                                  .                           (8.11)

 

Өз кезегінде егер тек тақ синусоидалары ғана бар функция 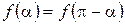 шартын қанағаттандырса, онда тақ кезде де  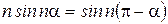екенін ескергенде, бұл жағдада да  b_n коэффиценттерін анықтау үшін мерзімнің төрттен бір бөлігі бойында  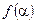қисығын пайдалану жеткілікті

 

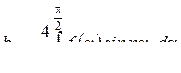                             .                                (8.12)

 

    Симметрия түрлері санамалау басын таңдауға байланысты болады. Егер санамалау басын таңдау мүмкін болса, онда оны ең көп симметрия алуға болатындай етіп таңдаған жөн.

 

8.3 Санамалау басын көшіру

Кейбір мерзімді синусоидалы емес 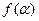 функциясы үшін а_n және b_n  коэффиценттері берілді делік, яғни берілген функцияны Фурье қатарына жіктеу белгілі

 

 

Егер санамалау басының координаттардың алғашқы басына қатысты β үзіндісіне оңға немесе солға орнын ауыстырсақ, онда жаңа координаттық жүйеге қатысты Фурье қатарына жіктеуді 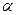-ны 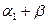-ге алмастыру арқылы жүзеге асырамыз, мұндағы  – жаңа координаттар жүйесіндегі абсцисса;  β-нің оң мәні санамалаудың жаңа бастауын оңға, ал теріс мәні – солға көшіруге сәйкес келеді.

Сонымен,

 

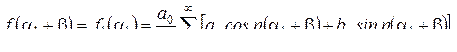        (8.13)

 

Егер біріншінің орнын абциссаның осі бойынша тұрақты мәнге ығысуының нәтижесінде алынатын басқа функцияға арналған Фурье қатарының коэффиценттері белгілі болғанда, бұл формула функцияларды Фурье қатарына жіктеуді тез табуға мүмкіндік береді.

 

8.4 Фурье қатарының кешенді формасы

Фурье қатарының тригонометриялық формасы кешендіге келесі түрде қайта түрленуі мүмкін

 

осыған байланысты (8.4) формуласында жақшаға алынған мән мына түрге келеді

 

,

 

 

(8.4) қатары келесі түрде жазылады

 

 

 (8.5) және (8.6) мәндеріне байланысты n-ге қатысты  а_n жұп, ал b_n  тақ, яғни n-нің теріс мәні кезінде өз белгісін сақтайды, ал b_n өзгертеді

 

, .

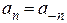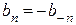Сондықтан, келесіні есепке алу арқылы

 

 

 

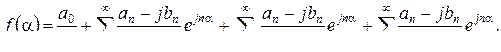
Осылайша, Фурье қатарының кешенді формада ие болатын түрі

 

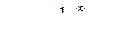                                                                           (8.14)

 

мұндағы кешенді коэффицент (кешенді амплитуда) (8.5) және (8.6) сәйкес келесі формула бойынша есептелінеді

 

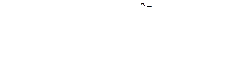                           .                    (8.15)

 

Жоғарыда көрсетілгендей, 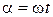 кезегінше  (8.14) қатарында  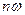бұрыштық жылдамдықпен қарама-қарсы бағытта айналатын векторлердің нақтылы осіне қатысты түйіндестірілген екі шексіз қатар болады. Түйіндестірілген векторлердің әрбір сыңарының геометриялық қосындысы 8.6 суретінде бейнеленген нақтылы мәнді ғана береді. Түйіндестірілген векторлердің екі шексіз қатарларын қосындылау нәтижесінде  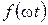нақтылы функциясы пайда болады.

 

 

 

8.6 Сурет –  Қарама-қарсы бағытта айналатын екі түйіндестірілген векторлердің қосындысы түріндегі синусоидалық функция

8.5 Фурье қатарын мерзімді синусоидалы емес үрдісті есептеуге қолдану

           Мерзімді синусоидалы емес ЭҚК-нің ықпалындағы электр тізбегіндегі тоқты табу қажет делік

 

.

 

Мұнда m индексімен гармоника амплитудалары белгіленген.Егер тізбек желілік болса, яғни r, L, М және С параметрлері өзгермейтін болса, онда тізбектегі тоқ беттестіру әдісімен әрбір қосындыланушы ЭҚК жеке түзетін тоқтарды қосындылау жолымен табылады.

 

                          ,                (8.16)

 

мұндағы

.

 

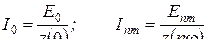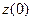дегеніміз нөлге тең жиілік кезіндегі тізбек кедергісі, яғни тұрақты тоққа деген кедергі;  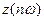–  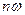жиілігі кезіндегі толық кедергі..

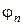 бұрышы тізбектің реактивті кедергісінің оның  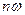жиілік кезіндегі активті кедергісіне деген қатынас арктангенсі түрінде анықталады.

Тізбек кезекті байланысқан r, L және С элементтерінен тұрған жағдайда

 

 

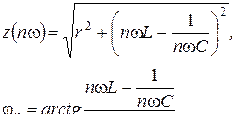
Сонда 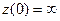, себебі тұрақты тоққа арналған тізбек ажыратылған.

Гармоника нөмірінің өсу шамасына байланысты, яғни 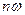 жиілігі ұлғайған сайын  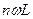индуктивті кедергі тура желі заңы бойынша өседі, ал  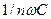 сыйымдылық кедергісі гипербола заңы бойынша кемиді. Сондықтан r және L кезекті байланысудан құралған тізбекте тоқ гармоникасы қайнаркөз ЭҚК-сіне қарағанда, әлсіз көрініс табады. Оған қарағанда тізбектегі r және С-тен құралған жоғары гармоникалар үлкен мәнге ие болуы мүмкін.

Индуктивті-сыйымдылықты аралас тізбекте 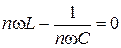 n-дік гармоника үшін резонанс құбылысы болады.

r, L және С элементерінен құралған жалпы жағдайда, реактивті де, активті де кедергілер 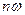 жиілігінің функциясы болып табылады (9.3 параграфті қара).

Әртүрлі гармоникалар мерзімі гармоника нөміріне кері пропорционал. Сондықтан, егер абциссалар осі бойынша 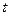 уақыты емес, ал  бұрышы алынса, онда негізгі гармониканың 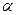 бұрышына сол абциссада 8.7 суретінде бейнеленгендей n –дік гармоникаға арналған  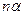бұрышы сәйкес келеді.

 

 

 

8.7 Сурет – Әртүрлі гармоникалар үшін бұрыш масштабтарының арақатынасы

 

      Тармақталған электр тізбектеріндегі периодты синусоидалы емес тоқ пен кернеулердің есебі кешенді формада жүзеге асырылады.

 Егер периодты синусоидалы емес ЭҚК (8.8) түрінің Фурье қатарының тригонометриялық формасында берілсе, онда ЭҚКмен тоқ келесі түрде келуі мүмкін

 

;

 

,

 

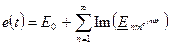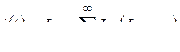мұндағы

 

 , .

 

    Сәйкесінше, мерзімді синусоидалы емес тоқты есептеудің кешенді формасы n-нің әртүрлі мәндеріне арналған ЭҚК-нің 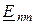 берілген кешенді амплитудаларына сәйкес  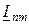тоқтың кешенді амплитудаларын табуда жатыр. Сонда жеке қосындылауыштарда біртексіз жиілік болатындығына байланысты кешенді амплитудалар қосылмайды, ал  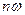әртүрлі бұрыштық жылдамдықпен айналатын векторлер проекциясы қосылады, яғни жеке гармоникалардың лездік мәндері қосылады.