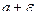«Аналитическая геометрия»
1. Векторы на плоскости. Основные понятия и определения.
2. Линейные операции над векторами в векторной форме. Проекция вектора.
3. Условия ортогональности и коллинеарности векторов на плоскости.
4. Векторы в пространстве, действия над векторами, заданными своими координатами в пространстве.
5. Векторное произведение векторов, формулы для его вычисления.
6. Свойства векторного произведения векторов.
7. Смешанное произведение векторов, геометрический смысл смешанного произведения векторов.
8. Прямая на плоскости, уравнение прямой, проходящей через две данные точки.
9. Каноническое уравнение прямой.
10. Уравнение прямой, проходящей через точку, параллельно данному вектору и уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.
11. Уравнение прямой в отрезках и параметрическое уравнение прямой.
12. Общее уравнение прямой на плоскости.
13. Угол между прямыми. Условия параллельности и перпендикулярности прямых на плоскости.
14. Уравнения плоскости в пространстве.
15. Уравнение прямой в пространстве (параметрическое, каноническое, через две данные точки, прямая как пересечение двух плоскостей).
16. Взаимное расположение плоскостей в пространстве, прямых в пространстве, прямой и плоскости в пространстве.
17. Кривые второго порядка.
18. Уравнение окружности.
19. Эллипс, его уравнения и характеристики.
20. Гипербола, ее уравнения и характеристики.
21. Парабола, ее уравнения и характеристики.
22. Поверхности второго порядка.
23. Сфера, ее уравнения и характеристики.
24. Эллипсоид, его уравнения и характеристики.
25. Гиперболоид, его уравнения и характеристики.
26. Параболоид, его уравнения и характеристики.
27. Как определяется расстояние между двумя точками?
28. Формула деления отрезка в данном отношении.
29. Как определить угол между двумя прямыми?
30. Как найти расстояние от точки до прямой?
31. Как определить угол между двумя плоскостями?
Тема 3. Введение в анализ
Последовательность, предел последовательности
Одним из основных понятий математического анализа является понятие функции.
Определение: Переменная 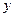 называется функцией от другой переменной
называется функцией от другой переменной 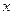 , если каждому значению
, если каждому значению 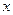 из некоторого множества по определенному правилу или закону ставится в соответствие одно или несколько значений переменной
из некоторого множества по определенному правилу или закону ставится в соответствие одно или несколько значений переменной 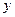 .
.
Если по некоторому закону каждому натуральному числу  поставлено в соответствие определенное число
поставлено в соответствие определенное число 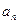 , то говорят, что задана числовая последовательность или функция натурального аргумента. Общий член последовательности
, то говорят, что задана числовая последовательность или функция натурального аргумента. Общий член последовательности  является функцией натурального аргумента
является функцией натурального аргумента  ,
, 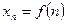 . Давая
. Давая 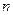 различные значения:
различные значения: 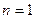 ,
, 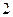 ,
, 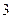 ,…, получим последовательность значений этой функции:
,…, получим последовательность значений этой функции:  ,
, 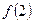 , …,
, …, 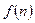 .
.
Функцию 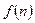 можно задать как аналитически, так и любым другим способом.
можно задать как аналитически, так и любым другим способом.
Определение: Число 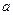 называется пределом последовательности
называется пределом последовательности 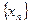 , если для любого положительного числа
, если для любого положительного числа 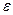 найдется такой номер
найдется такой номер 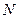 , выполняется неравенство
, выполняется неравенство  .
.
Геометрически определение предела последовательности можно сформулировать следующим образом: число 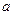 является пределом последовательности
является пределом последовательности 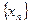 , если какова бы ни была
, если какова бы ни была 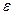 – окрестность точки
– окрестность точки 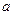 , начиная с некоторого номера все точки
, начиная с некоторого номера все точки 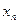 попадут в эту окрестность, т.е. вне интервала
попадут в эту окрестность, т.е. вне интервала 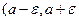 ) останется лишь конечное число членов последовательности.
) останется лишь конечное число членов последовательности.
 |




|
| ||||||
| |||||||
Тот факт, что последовательность  имеет предел, равный
имеет предел, равный 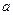 , записывают:
, записывают: 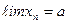 . Говорят, что последовательность сходится или имеет конечный предел.
. Говорят, что последовательность сходится или имеет конечный предел.
Определение: Последовательность  называется бесконечно большой, если для любого числа
называется бесконечно большой, если для любого числа  найдется номер
найдется номер 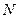 , такой, что для всех
, такой, что для всех  выполняется неравенство
выполняется неравенство 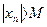 .
.
Геометрически это означает, что какое бы мы число 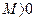 ни взяли, все члены последовательности, кроме конечного числа их, лежат вне отрезка
ни взяли, все члены последовательности, кроме конечного числа их, лежат вне отрезка  .
.
Тот факт, что 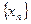 бесконечно большая записывают, следующим образом
бесконечно большая записывают, следующим образом 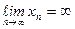 . Последовательность расходится, если она не имеет предела или ее предел равен бесконечности.
. Последовательность расходится, если она не имеет предела или ее предел равен бесконечности.
Определение: Последовательность 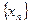 называется бесконечно малой, если
называется бесконечно малой, если 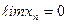 .
.
Из определения предела последовательности непосредственно получаем, что последовательность 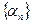 будет бесконечно малой, если для любого положительного числа
будет бесконечно малой, если для любого положительного числа  найдется число
найдется число  , такое, что для
, такое, что для  выполняется неравенство
выполняется неравенство 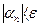 . Общие члены бесконечно малых последовательностей будем обозначать буквами греческого алфавита, например
. Общие члены бесконечно малых последовательностей будем обозначать буквами греческого алфавита, например 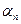 ,
, 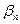 ,
, 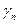 , …
, …
Если последовательность 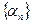 бесконечно малая и все ее члены отличны от нуля, то последовательность
бесконечно малая и все ее члены отличны от нуля, то последовательность 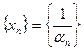 – бесконечно большая, и обратно, если последовательность
– бесконечно большая, и обратно, если последовательность 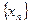 ,
, 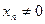 , бесконечно большая, то последовательность
, бесконечно большая, то последовательность 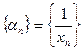 – бесконечно малая.
– бесконечно малая.
Суммой, разностью, произведением и частным двух последовательностей 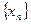 ,
, 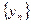 называются соответственно последовательности
называются соответственно последовательности 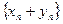 ,
, 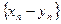 ,
,  ,
, 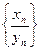 . При делении следует сделать оговорку, что все члены последовательности делителя отличны от нуля.
. При делении следует сделать оговорку, что все члены последовательности делителя отличны от нуля.
Для последовательностей справедливы следующие теоремы:
1. Алгебраическая сумма двух сходящихся последовательностей есть сходящаяся последовательность, ее предел равен соответствующей сумме пределов данных последовательностей, т.е. 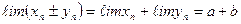 .
.
2. Произведение двух сходящихся последовательностей есть сходящаяся последовательность, ее предел равен произведению пределов данных последовательностей  .
.
3. Если последовательности  и
и  сходятся, то последовательность
сходятся, то последовательность  сходятся и ее предел равен отношению пределов последовательностей
сходятся и ее предел равен отношению пределов последовательностей  и
и 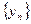 , т.е.
, т.е. 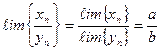 , причем
, причем 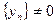 и
и 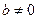 .
.
При вычислении пределов могут встретиться «неопределенности» вида  ;
;  ;
;  и другие.
и другие.
Пример 1. Вычислить предел: 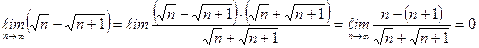 .
.
Пример 2. Вычислить предел:

Так как, 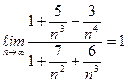 , то данная последовательность – бесконечно большая, т.е.
, то данная последовательность – бесконечно большая, т.е. 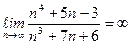 .
.
Предел функции
Пусть функция 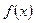 определена в некоторой окрестности точки
определена в некоторой окрестности точки 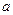 , т.е. в некотором интервале, содержащем
, т.е. в некотором интервале, содержащем 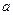 , кроме, быть может, самой точки
, кроме, быть может, самой точки 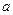 . В точке
. В точке 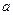 функция может быть и не определена.
функция может быть и не определена.
Определение: Число  называется пределом функции
называется пределом функции 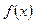 при
при  , стремящемся к
, стремящемся к 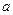 (или в точке
(или в точке 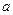 ), если для любого положительного числа
), если для любого положительного числа  найдется такое положительное число
найдется такое положительное число 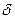 , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию 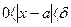 выполняется неравенство
выполняется неравенство 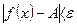 .
.
Из определения следует, что для любого 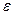 > 0 (положительное число
> 0 (положительное число  может быть сколь угодно малым) существует
может быть сколь угодно малым) существует  такое, что для всех точек симметричного относительно
такое, что для всех точек симметричного относительно 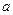 интервала
интервала  ,
, 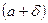 ,
, 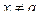 , значения функции не выходят из
, значения функции не выходят из 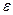 – окрестности точки
– окрестности точки  .
.
Тот факт, что предел функции при 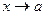 равен
равен  , записывают так:
, записывают так:  или
или 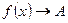 при
при 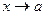

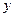
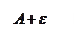
 |  | ||










 |
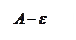
 |  |  |








| |
|
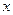
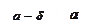 |
|
На следующем рисунке функция не имеет предела при 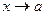
| |
|











Пример 3. Докажем, а что функция  при
при 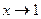 имеет предел, равный 5.
имеет предел, равный 5.
Для доказательства установим, что какое бы положительное число 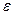 мы не взяли, можно найти такое положительное число
мы не взяли, можно найти такое положительное число 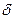 , что для всех значений
, что для всех значений  , отличающихся по абсолютной величине от числа
, отличающихся по абсолютной величине от числа  меньше чем на
меньше чем на 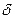 , будет справедливо неравенство
, будет справедливо неравенство 
 . Отсюда
. Отсюда 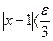 . Поэтому, если взять
. Поэтому, если взять 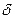 , удовлетворяющее условию
, удовлетворяющее условию  , то
, то 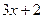 будет отличаться от числа
будет отличаться от числа 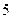 по абсолютной величине меньше на
по абсолютной величине меньше на 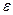 при
при 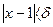 . А это означает, что
. А это означает, что  .
.
Определим предел функции при стремлении аргумента к бесконечности.
Определение: Число 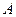 называется пределом функции
называется пределом функции 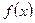 при
при 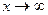 , если для любого
, если для любого 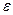 > 0 найдется такая окрестность символа
> 0 найдется такая окрестность символа  , что все значения функции
, что все значения функции 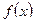 в точках этой окрестности отличаются от числа
в точках этой окрестности отличаются от числа 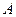 по абсолютной величине меньше чем на
по абсолютной величине меньше чем на  .
.
Если 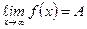 , то график функции
, то график функции 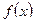 асимптотически приближается к прямой
асимптотически приближается к прямой  при стремлении
при стремлении  к бесконечности как по положительным, так и по отрицательным значениям (смотри рисунок).
к бесконечности как по положительным, так и по отрицательным значениям (смотри рисунок).
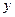
 |  | ||||
 | |||||

|


 2020-10-12
2020-10-12 247
247