Будем говорить, что на плоскости задана декартова прямоугольная система координат, если задан единичный (масштабный) отрезок, а также пара взаимно перпендикулярных осей. Обычно горизонтальную ось называют осью абсцисс, вертикальную ось – осью ординат. Точку О пересечения этих осей будем называть началом координат.
Введение на плоскости декартовой прямоугольной системы координат позволяет установить взаимно однозначное соответствие между множеством всех точек плоскости и множеством пар действительных чисел. Это соответствие дает возможность сводить изучение множеств точек плоскости к изучению множеств пар действительных чисел, т.е. применять к изучению вопросов геометрии алгебраические методы.
Рассмотрим расстояние (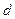 ) между двумя точками
) между двумя точками 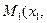
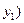 и
и 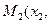
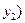 плоскости находятся по формуле:
плоскости находятся по формуле:
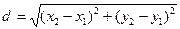
Координаты 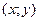 точки
точки  , делящей отрезок с концами
, делящей отрезок с концами 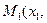
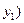 и
и 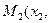
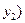 в отношении
в отношении 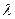 находятся по формуле:
находятся по формуле:
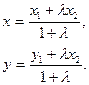
Координаты  точки
точки 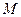 – середины отрезка с концами
– середины отрезка с концами 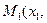
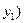 и
и 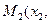
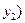 находятся по формуле:
находятся по формуле:
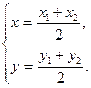
Уравнение прямой:
а) с угловым коэффициентом 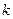 и начальной ординатой
и начальной ординатой 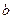 :
: 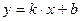 ;
;
б) проходящей в данном направлении (с угловым коэффициентом 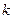 ) через данную точку
) через данную точку 
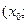
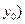 :
: 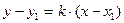 ;
;
в) проходящей через две данные точки 
 и
и 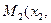
 :
:
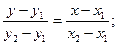
г) с угловым коэффициентом 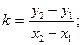
д) в отрезках: 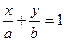
(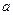 и
и 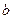 – соответственно отрезки, отсекаемые на осях
– соответственно отрезки, отсекаемые на осях 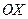 и
и 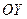 );
);
е) Общее уравнение прямой: 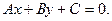
Рассмотрение 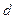 от точки
от точки 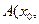
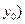 до прямой
до прямой 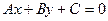 находится по формуле:
находится по формуле:
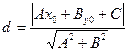
Если две прямые заданы уравнениями  и
и 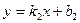 или
или 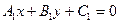 и
и 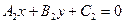 , то угол
, то угол 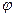 между прямыми находится из соотношения
между прямыми находится из соотношения 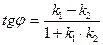 или
или 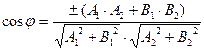 .
.
Условие параллельности двух прямых:
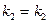 или
или 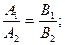
Условие перпендикулярности двух прямых:
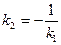 или
или 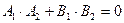
Точка пересечения двух прямых находится из решения системы:
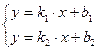 или
или 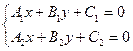
Задача 1.
Даны величины  .
. 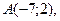

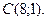 Составить уравнения:
Составить уравнения:
а) сторон треугольника;
б) медианы, высоты и биссектрисы проведенных из вершины 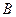 .
.
Решение:
а) Составим уравнение стороны 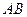 точек
точек 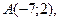
 . Подставим координаты в уравнение
. Подставим координаты в уравнение 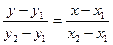 .
.
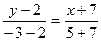 . Преобразуем это равенство.
. Преобразуем это равенство.
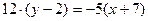
 или
или 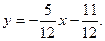
Для стороны  имеем равенство
имеем равенство
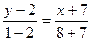
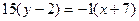
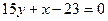 или
или 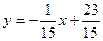 .
.
Аналогично, сторона 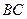 задается уравнением
задается уравнением 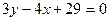 или
или 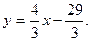
б) Найдем уравнение медианы 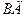 , где
, где 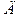 – середина отрезка
– середина отрезка 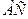
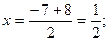
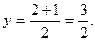

Угловой коэффициент к прямой 

Медиана  имеет
имеет 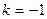 проходит через точку
проходит через точку 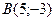 . Получим уравнение медианы
. Получим уравнение медианы  :
: 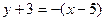 или
или 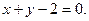
Найдем уравнение высоты  Угловой коэффициент прямой
Угловой коэффициент прямой 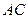
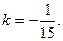 На основании угловая перпендикулярности двух прямых
На основании угловая перпендикулярности двух прямых 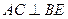

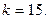
Уравнение высоты 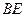 примет вид:
примет вид:
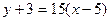 или
или 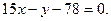
Найдем уравнение биссектрис 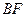 . По свойству биссектрисы расстояния ее от любой точки
. По свойству биссектрисы расстояния ее от любой точки 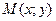 до сторон
до сторон 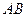 и
и 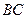 равны, получим
равны, получим
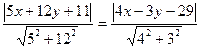
Записанному уравнению удовлетворяют два: 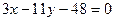 и
и 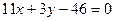 .
.
Чертежу задачи удовлетворяет второе уравнение, так как биссектриса  образует тупой угол с осью
образует тупой угол с осью 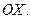
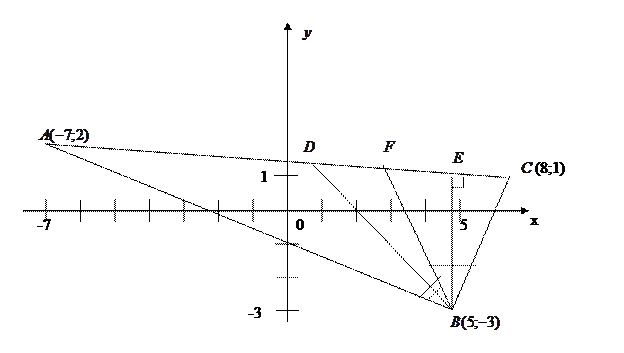

Задача 2.
В  , заданном координатами своих вершин:
, заданном координатами своих вершин: 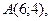

 Найти:
Найти:
а) длину медианы 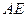 , проведенной из вершины
, проведенной из вершины  ;
;
б) длину высоты  , опущенной из вершины
, опущенной из вершины 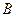 ;
;
 в) точку пересечения медианы
в) точку пересечения медианы  и высоты
и высоты 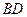 .
.
Решение:
Сделаем схематический чертеж  . Определим координаты точки
. Определим координаты точки  , как точки, делящей отрезок
, как точки, делящей отрезок 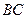 пополам:
пополам:
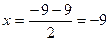 ,
, 
Длину медианы определим по формуле расстояния между двумя точками  и
и 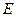 :
:

Составим уравнение стороны 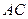 используя уравнение прямой, проходящей через две точки
используя уравнение прямой, проходящей через две точки  и
и  , а длину
, а длину 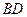 определим по формуле расстояния точки
определим по формуле расстояния точки 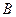 до прямой
до прямой  :
:
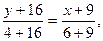
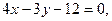
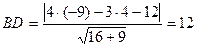
Составим уравнение медианы 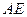 , используя уравнение прямой, проходящей через две точки
, используя уравнение прямой, проходящей через две точки  и
и 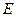 :
:
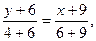

Уравнение высоты  составим по точке и угловому коэффициенту
составим по точке и угловому коэффициенту 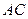 . Угловой коэффициент прямой
. Угловой коэффициент прямой 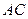
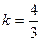 , следовательно, угловой коэффициент прямой
, следовательно, угловой коэффициент прямой 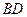 , перпендикулярной к
, перпендикулярной к  , равен
, равен 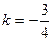 . Уравнение прямой
. Уравнение прямой 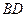 имеет вид:
имеет вид:


Для определения искомой точки 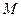 пересечения медианы и высоты решаем систему уравнений:
пересечения медианы и высоты решаем систему уравнений:
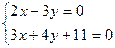
При решении находим, что 
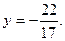
 2020-10-12
2020-10-12 204
204








