Нахождение производной функции называется дифференцированием.
Основные правила:
Производная алгебраической суммы функций равна алгебраической сумме производных этих функций, т.е. 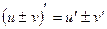 , где
, где  ,
, 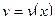 – дифференцированные функции.
– дифференцированные функции.
Постоянный множитель 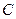 можно выносить за знак производной.
можно выносить за знак производной.

Производные от произведения и частного равны соответственно
 и
и  при условии, что функция
при условии, что функция 
отлична от нуля в рассматриваемой точке.
Определение: Пусть  ,
,  , причем область изменения второй функции входит в область определения первой. Тогда
, причем область изменения второй функции входит в область определения первой. Тогда 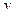 является сложной функцией независимой переменной
является сложной функцией независимой переменной  ,
, 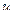 – промежуточная переменная.
– промежуточная переменная.
Производная сложной функции по независимой переменной равна произведению этой функции по промежуточной переменной на производную промежуточной переменной по независимой переменной

При нахождении производных функций полезно знать формулы дифференцирования основных элементарных функций
1. 

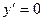
2. 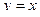
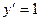
3. 

4. 

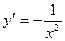
5. 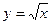
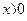
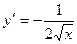
6. 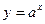
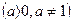
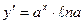


7. 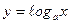

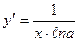
8. 
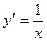
9. 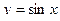
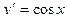
10. 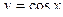

11. 
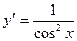
12. 

13. 

14. 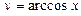

15. 
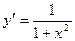
16. 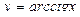
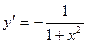
Если зависимость между 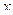 и
и  задана в неявной форме уравнением
задана в неявной форме уравнением 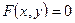 , то для нахождения производной функции
, то для нахождения производной функции  необходимо продифференцировать по
необходимо продифференцировать по 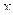 обе части данного уравнения, рассматривая
обе части данного уравнения, рассматривая  как функцию от
как функцию от 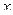 . Из полученного уравнения первой степени (относительно
. Из полученного уравнения первой степени (относительно 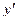 ) находится
) находится 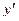 .
.
Если функция аргумента  задана параметрически уравнениями
задана параметрически уравнениями  и
и 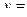
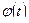 , то
, то 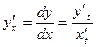 .
.
Пример 1.
Найти производные функций:
а) 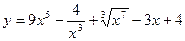
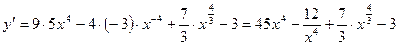
б) 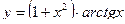
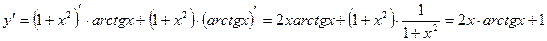
Пример 2.
Найти производную от функции, заданной неявно: 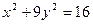
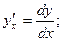 Продифференцируем обе части данного уравнения по
Продифференцируем обе части данного уравнения по 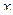 . Получим
. Получим  Решим последнее уравнение относительно
Решим последнее уравнение относительно 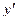 , получим
, получим 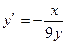 .
.
Пример 3.
Найти производную функции, заданную параметрически:
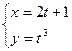
Т.к.  , то получим
, то получим 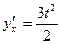 .
.
Пусть 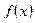 дифференцируема в точке
дифференцируема в точке  .
.
Определение: Дифференциалом функции 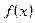 в точке
в точке  называется главная, линейная относительно
называется главная, линейная относительно 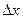 , часть приращения функции.
, часть приращения функции.
Дифференциал функции  обозначается через
обозначается через 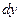 или
или  . Из определения следует, что
. Из определения следует, что 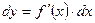 .
.
Дифференциал функции 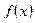 в точке
в точке  равен произведению производной функции в этой точке на дифференциал независимой переменной.
равен произведению производной функции в этой точке на дифференциал независимой переменной.
Из определения дифференциала следует также, что нахождение производных или дифференциалов по существу представляет собой одну и ту же задачу.
 2020-10-12
2020-10-12 166
166








