2020-10-12
123
Теорема Ролля. Если функция 
непрерывна на отрезке 
, дифференцируема на интервале 
и значения функции на концах отрезка равны, 
, то на интервале 
существует точка с, 
, в которой производная функции равна 
, 
.
Геометрический смысл теоремы Ролля: если условия теоремы выполняются, то на интервале существует такая точка 
, что в соответствующей ей точке касательная к кривой 
параллельна оси 
.
Из теоремы Ролля следует важное свойство: между двумя нулями функции находится по крайней мере один нуль ее производной.
Теорема Лагранжа. Если функция непрерывна на отрезке 
и дифференцируема на интервале , то на этом интервале найдется по крайней мере одна точка , такая, что 
.
Или, что то же, если на некотором отрезке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Отношение 
равно угловому коэффициенту секущей.
Теорема Коши. Если функции и 
непрерывны на отрезке , дифференцируемы на интервале и 
на , то существует по крайней мере одна точка , , такая, что 
, т.е. отношение приращений функций на данном отрезке равно отношению их производных в точке с.
Следующая теорема, называемая правилом Лопиталя, практически облегчает задачу нахождения этого предела.
Есл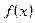и 
и 
дифференцируемы вблизи 
, непрерывны в точке , производная функции отлична от нуля вблизи и 
, то предел отношения функций при 
равен пределу отношения их производных, если последний (конечный или бесконечный) существует:
.
Пример 4.
Найти пределы
а) 
.
б) 
.
