2020-10-12
134
Пусть в точке 
кривая 
имеет касательную, не параллельную 
.
Определение: Кривая называется выпуклой (вогнутой) в точке 
, если в некоторой окрестности этой точки кривая расположена ниже (выше) касательной, проведенной в точке .
Определение: Точка называется точкой перегиба кривой , если с одной стороны от кривая вогнута, а с другой стороны кривая выпукла.
Таким образом, если в точке кривая меняет выпуклость на вогнутость (или наоборот), то точка является точкой перегиба. Из этого определения непосредственно следует, что касательная в точке перегиба кривой пересекает эту кривую.
Для кривых 
можно сформулировать правила исследования на выпуклость, вогнутость и перегиб:
1. Находим точки, в которых 
или вторая производная функции 
не существует. Такие точки называются критическими точками функции 
по второй производной.
2. Эти точки разделят область определения функции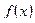 
на интервалы, в каждом из которых 
сохраняет знак.
Если в рассматриваем интервале 
, тот это интервал вогнутости, если же 
, то это интервал выпуклости.
Точки перегиба выделяются автоматически: они разделяют интервалы выпуклости и вогнутости.
Асимптоты плоских кривых
Определение: Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат или, что то же, когда расстояние точки от начала координат неограниченно растет.
Для того чтобы кривая имела асимптоту 
, необходимо и достаточно, чтобы существовали конечные пределы
, 
.
Если 
и 
– конечно, то асимптота 
– горизонтальная.
Определение: Прямая называется горизонтальной асимптотой, если существует конечный предел при 
равный , т.е.
.
Прямая 
, если 
.
Пример 1.
Найти асимптоты кривой 
.
Область определения функции 
, т.е. 
– вертикальная асимптота.
Все остальные асимптоты (если они есть) имеют вид 
. Найдем 
и .
и
, 
– асимптота.
