Возрастание и убывание функций

Определение: Функция  называется возрастающей на данном промежутке, если для любых двух точек 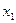 и 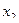 этого промежутка из неравенства  следует неравенство .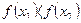

Необходимое условие возрастания и убывания дифференцируемой функции:

Если дифференцируемая функция 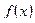 возрастает на данном промежутке, то в любой точке  этого промежутка 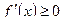. Если дифференцируемая функция  убывает на данном промежутке, то в любой точке  этого промежутка .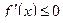

Достаточное условие возрастания и убывания функции:

Пусть  – дифференцируемая функция на некотором промежутке. Если в каждой точке  данного промежутка 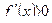, то функция  возрастает на этом промежутке. Если в каждой точке  данного промежутка , то функция  убывает на этом промежутке.

Интервалы, на которых функция возрастает (убывает), называется интервалами монотонности функции. Точка, в которой 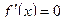, называется такой точкой стационарности функции .

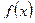Сформулируем правило исследования функций на возрастание и убывание функции:

1. Находим точки из области определения функции, в которых производная функции равна нулю или не существует. Эти точки называют критическими для функции 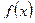 по первой производной. Критические точки разбивают область определения функции  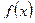на интервалы, на каждом из которых производная  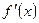сохраняет знак.

2. Исследуем знак 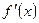 на каждом из этих интервалов. Если на рассматриваемом интервале 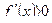, то это интервал возрастания, если же , то это интервал убывания.

Экстремумы  функции

Определение: Точка  называется точкой максимума функции 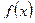 на некотором промежутке , если существует такая окрестность точки , что для всех  этой окрестности выполняется неравенство 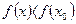. Точка  называется точкой минимума функции , если существует такая окрестность точки , что для всех  этой окрестности выполняется неравенство .

Точки максимума и минимума называются точками экстремума. Значение функции 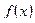 в точках максимума (минимума) называют максимумом (минимумом) функции, или экстремумом функции.

Необходимое условие экстремума дифференцируемой функции:

Если дифференцируемая функция 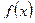 имеет в точке  экстремум, то .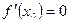

Достаточные условия существования экстремума кратко можно сформулировать так: если функция  непрерывна в точке и в некоторой ее окрестности и ее производная 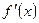 при переходе через  меняет знак с «+» на «-», то функция 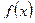 в точке  имеет максимум; если же производная при переходе через точку  меняет знак с минуса на плюс, то в точке  функция  имеет минимум.

Для нахождения экстремума функции нужно:

1. Найти точки, принадлежащие области определения функции , в которых ее производная 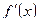 равна 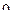 или не существует, т.е. найти критические точки функции по первой производной.

2. Исследовать знак 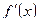в некоторой окрестности каждой критической точки. При этом, если  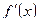меняет знак при переходе через такую точку, то функция в этой точке имеет экстремум. Если же 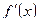не меняется при переходе через рассматриваемую точку, то функция  не имеет экстремума в этой точке.