Алгоритм симплексного метода

Графический метод решения задачи линейного программирования является простым и наглядным. Однако главным его недостатком является то, что этот метод применяется только для задач с 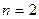 переменными. Симплексный метод является универсальным, так как позволяет решить практически любую задачу линейного программирования, записанную в каноническом виде. Опорным решением называется базисное неотрицательное решение.

Алгоритм симплексного метода.

1) Математическая модель задачи должна быть канонической. Если она не каноническая. То ее надо привести к каноническому виду.

2) Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплексную таблицу. Все строки таблицы 1-го шага, за исключением строки 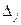(индексная строка), заполняем по данным системы ограничений и целевой функции.

 

ni	Aj	n1	n2	…	nm	nm+1	…	nn	L(x)
		x1	x2		xm	xm+1		xn	bi
n1	x1	1	0		0	h1,m+1		h1,n	f1
n2	x2	0	1		0	h2,m+1		h2,n	f2
…	…	…	…	…	…	…	…	…	…
nm	xm	0	0		1	hm,m+1		hm,n	f3
		0	0	…	0		10

 

Индексная строка для переменных находится по формуле

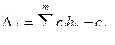 и по формуле

 для свободного члена.

Возможны следующие случаи при решении задачи на максимум:

- если все оценки 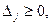 то найденное решение оптимальное;

- если хотя бы одна оценка  но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращением, т.к. 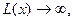 т.е. целевая функция неограниченна в области допустимых решений ОДР;

- если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;

- если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Если хотя бы одна оценка  то 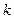-й столбец принимаем за ключевой. За ключевую строчку принимаем ту, которая соответствует минимальное отношение свободных членов  к положительным коэффициентам 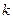-го столбца.

Этот элемент, находящийся на пересечении ключевых строки и столбца, называется ключевым элементом.

3) Заполняем симплексную таблицу 2-го шага:

- переписываем ключевую строчку, разделив ее на ключевой элемент;

- заполняем базисные столбцы;

- остальные коэффициенты таблицы находим по правилу «прямоугольника».

Оценки модно считать по приведенным выше формулам. Получаем новое опорное решение, которое проверяем на оптимальность и т.д.

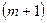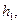
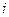Правило «прямоугольника» заключается в следующем. Путь ключевым элементом 1-го шага является элемент 1-й строчки -го столбца . Тогда элемент -й строки 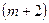-го столбца 2-го шага – обозначим его 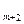 – согласно правилу «прямоугольника» выражается формулой

,

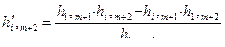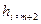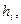
где , ,  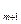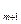– элементы первого шага.

Примечание. Если целевая функция  требует нахождения минимального значения, то критерием оптимальности задачи является неположительность оценок 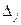  при всех .

 

Пример 2. Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя разными способами.

Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в таблице:

Производственные ресурсы	Расход ресурсов за 1 месяц при работе		Общий ресурс
	1-ым сп.	2-ым сп.
сырье	1	2	4
оборудование	1	1	3
электроэнергия	2	1	8

При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором – 4 тыс. изделий. Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?

Решение.

Составим математическую модель: 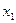 – время работы предприятия 1-ым способом;  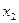– время работы предприятия 2-ым способом.

 при ограничениях:

Приведем задачу к каноническому виду:

 при ограничениях:

Составляем симплексную таблицу 1-го шага.

Получим решение:  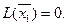В индексной строчке  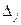имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменой 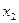, а за ключевую строку взять строку переменой 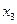, где

Ключевым моментом является 2.

Вводим в столбец базисной переменной 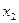, выводим 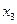. Составляем симплексную таблицу 2-го шага.

Вводим в столбец базисной переменной 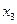. Составляем симплексную таблицу 2-го шага.

 

ni	Aj	3	4	0	0	0	L (x)
		X1	X2	X3	X4	X5	bi
4	X2	½	1	½	0	0	2
0	X4	½	0	-1/2	1	0	1
0	X5	3/2	0	-1/2	1	1	6
		-1	0	2	0	0	8

 

Получим 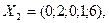 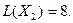В индексной строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является ½. Составляем симплексную таблицу 3-го шага.

 

ni	Aj	3	4	0	0	0	L (x)
		X1	X2	X3	X4	X5	bi
4	X2	0	1	1	-1	0	2
3	X1	1	0	-1	2	0	1
0	X5	0	0	1	-3	1	6
		0	0	1	2	0	10

Все оценки свободных переменных 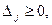 следовательно, найденное опорное решение является оптимальным:

Таким образом, по правому способу предприятие должно работать два месяца, по второму один месяц, при этом максимальный выпуск продукции составляет 10 тыс.ед.

Транспортная  задача

Транспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозов.

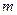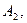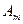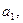
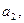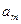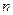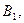
В общем виде задачу можно представить следующем образом: в  пунктах производства  …,  имеется однородный груз в количестве соответственно  …, . Этот груз необходимо доставить в  пунктов назначения  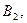…,  в качестве соответственно  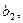…, 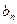. Стоимость перевозки единицы груза (тариф) из пункта  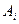в пункт  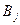равна .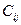

Потребуется составить план перевозок, позволяющий вывести все грузы и имеющий минимальную стоимость.

Если 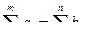, то задача называется закрытой (ЗТЗ).

Если , то задача называется открытой (ОТЗ).

Обозначим через  количество груза, перевозимого из пункта 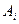 в пункт .

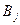Рассмотрим ЗТЗ. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения.

 

 

			…
			…
			…
...	…	…	…	…
			…

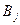
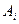
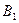
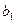
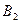
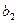
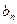
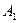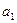
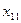
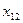
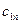
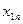
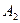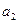
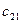
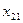
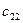
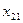
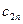
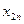
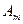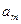
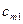
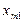
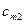
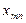
Математическая модель закрытой транспортной задачи имеет вид:

при ограничениях:

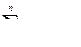
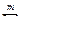
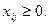
Оптимальным решением является матрица 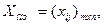 удовлетворяющая системе ограничений и доставляющая минимум целевой функции.

Для решения транспортной задачи разработан специальный метод, имеющий этапы:

-  нахождение исходного опорного решения;

-  проверка этого решения на оптимальность;

-  переход от одного опорного решения к другому.

Нахождение  исходного  опорного  решения

Условия задачи и ее исходное опорное решение будем записывать в распределительную таблицу. Клетки, в которые поместим грузы, называются занятыми, им соответствуют базисные переменные опорного решения. Остальные клетки незанятые или пустые, им соответствуют свободные переменные. В верхнем правом углу каждой клетки будем записывать тарифы. Существует несколько способов нахождения исходного опорного решения: метод минимального тарифа; метод северо-западного угла и др.

Рассмотрим метод минимального тарифа. Согласно этому методу, грузы распределяются в первую очередь в те клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем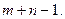

В этом случае недостающие их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми.

Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждой строке и столбце было не менее чем по одной занятой клетке.

Пример 3. На складах 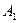, , 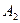 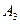имеются запасы продукции в количествах 90; 400; 110 т соответственно. Потребители 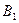, , 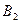 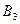должны получить эту продукцию в количествах 140; 300; 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (усл. ед.)

 

Проверим, является ли данная транспортная задача закрытой:

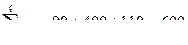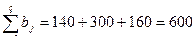т,

т,

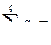
, следовательно, данная транспортная задача закрытая. Найдем исходное опорное решение по методу минимального тарифа.

 

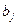
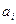
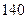
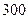
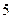
			5

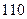
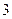
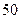
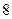
Число занятых клеток равно 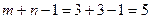, т.е. условие невырожденности выполнено. Получим исходное опорное решение, которое запишем в виде матрицы:

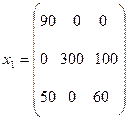
Стоимость перевозки при исходном опорном решении составляет:

 усл. ед.

Метод  потенциалов

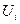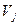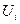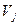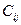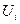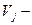
Найденное исходное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение ТЗ является оптимальным, то ему соответствует система  действительных чисел  и , удовлетворяющих условиям + = для занятых клеток и + для свободных клеток.

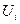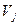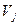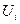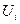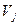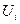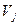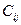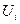Числа  и  называют потенциальными.В распределительную таблицу добавляют строчку  и столбец . Потенциалы  и  находят из равенства + = , справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например , тогда остальные потенциалы определяются однозначно. Так, если известен потенциал , то 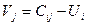; если известен потенциал 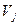, то . Обозначим 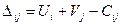. Эту оценку называют оценкой свободных клеток. Если 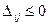, то опорное решение является оптимальным. Если хотя бы одна из оценок , то опорное решение не является оптимальным и его можно опорного решения к другому.

Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец 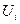 и столбец 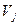. Полагая , запишем это значение в первом столбце таблицы

 

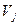
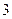
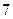
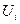
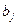
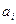
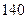
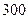
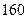
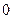
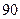
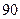
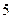
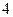
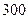
				5   100

.

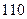
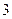
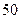
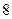
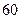
Для занятых клеток составляем систему уравнений:

.

Отсюда , , , , .

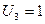Найденные значения потенциалов заносим в таблицу. Вычислим оценки свободных клеток:

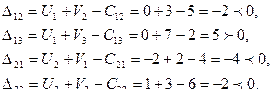
Получили одну оценку 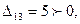 следовательно, исходное опорное решение не является оптимальным и его модно улучшить.

Наличие положительной оценки свободной клетки 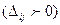 при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение неоптимально и для уменьшения значения целевой функции надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.

Для свободной клетки с  строится цикл, все вершины которого кроме одной находится в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла становится (+), затем поочередно проставляют знаком (–) и (+). У вершин со знаком (–) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+) и отнимают от грузов у вершин со знаком (–). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение.

		–	–	+
		–
			–	–

 

 

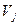
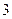
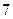
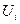
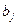
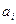
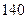
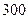
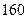
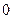
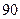
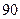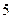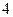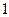
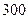
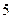
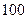
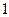
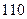
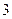
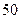
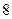
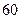
Новое опорное решение

		–	–	+
		+		–
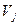
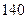
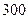
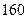
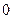
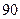
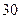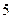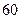
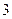
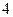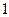
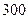
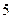
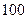
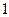
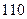
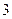
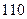
			–	8 –

 

Произведем перераспределение грузов. Получим новое решение. Проверим его на оптимальность.

 

		–	–
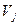
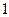
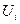
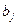
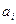
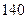
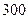
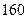
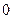
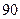
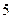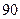
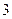
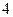
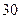
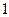
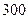
				5 70
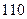
			–	8 –

 

 

 

Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Итак,

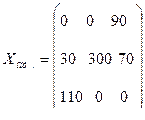
Стоимость транспортных расходов равна: 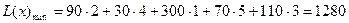 усл. ед.

По сравнению с исходными опорным решением транспортные расходы уменьшились на 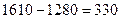 усл. ед.

При открытой ТЗ сумма запасов не совпадает с суммой потребностей. В этом случае вводят фиктивного поставщика или потребителя. При введении фиктивного поставщика или потребителя ОТЗ становится закрытой и решается по ранее рассмотренному алгоритму для ЗТЗ, причем тарифы, соответствующие фиктивному поставщику или потребителю, больше или равны наибольшему из всех транспортных тарифов, иногда их считают равными нулю.

В целевой функции фиктивный поставщик или потребитель не учитывается.